
自然语言处理:最大熵和对数线性模型
Natural Language Processing: Maximum Entropy and Log-linear Models
作者:Regina Barzilay(MIT,EECS Department, October 1, 2004)
译者:我爱自然语言处理(www.52nlp.cn ,2009年5月14日)
三、 最大熵模型详述
g) GIS算法(Generative Iterative Scaling)
i. 背景:
最原始的最大熵模型的训练方法是一种称为通用迭代算法GIS (generalized iterative scaling) 的迭代算法。GIS 的原理并不复杂,大致可以概括为以下几个步骤:
1. 假定第零次迭代的初始模型为等概率的均匀分布。
2. 用第 N 次迭代的模型来估算每种信息特征在训练数据中的分布,如果超过了实际的,就把相应的模型参数变小;否则,将它们变大。
3. 重复步骤 2 直到收敛。
GIS 最早是由 Darroch 和 Ratcliff 在七十年代提出的。但是,这两人没有能对这种算法的物理含义进行很好地解释。后来是由数学家希萨(Csiszar) 解释清楚的,因此,人们在谈到这个算法时,总是同时引用 Darroch 和Ratcliff 以及希萨的两篇论文。GIS 算法每次迭代的时间都很长,需要迭代很多次才能收敛,而且不太稳定,即使在 64 位计算机上都会出现溢出。因此,在实际应用中很少有人真正使用 GIS。大家只是通过它来了解最大熵模型的算法。
八十年代,很有天才的孪生兄弟的达拉皮垂(Della Pietra)在 IBM 对 GIS 算法进行了两方面的改进,提出了改进迭代算法 IIS(improved iterative scaling)。这使得最大熵模型的训练时间缩短了一到两个数量级。这样最大熵模型才有可能变得实用。即使如此,在当时也只有 IBM 有条件是用最大熵模型。(以上摘自Google吴军《数学之美系列16》)
ii. 目标(Goal):寻找遵循如下约束条件的此种形式
iii. GIS约束条件(GIS constraints):
1、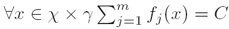
其中C是一个常数(where C is a constant (add correctional feature))
2、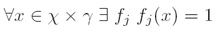
iv. 定理(Theorem):下面的过程将收敛到p*∈P∩Q(The following procedure will converge to p*∈P∩Q):
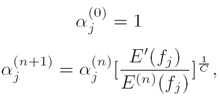
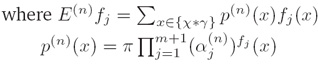
v. 计算量(Computation)
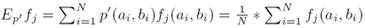
其中S={(a1,b1),...,(aN,bN)}是训练样本(where S is a training sample)
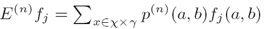
因为有太多可能的(a,b),为了减少计算量,因而采用下面的公式近似计算:
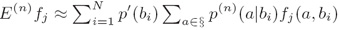
时间复杂度(Running time):O(NPA)
其中N训练集规模,P是预期数,A是对于给定事件(a,b)活跃特征的平均数(where N is the training set size, P is the number of predictions, and A is the average number of features that are active for a given event (a,b))
四、 最大熵分类器(ME classifiers)
a) 可以处理很多特征(Can handle lots of features)
b) 存在数据稀疏问题(Sparsity is an issue)
i. 应用平滑算法和特征选择方法解决(apply smoothing and feature selection)
c) 特征交互(Feature interaction)?
i. 最大熵分类器并没有假设特征是独立的(ME classifiers do not assume feature independence)
ii. 然而,它们也没有明显的模型特征交互(However, they do not explicitly model feature interaction)
五、 总结(Summary)
a) 条件概率建模与对数线性模型(Modeling conditional probabilities with log-linear models)
b) 对数线性模型的最大熵性质(Maximum-entropy properties of log-linear models)
c) 通过迭代缩放进行优化(Optimization via iterative scaling)
一些实现的最大熵工具(Some implementations):
http://nlp.stanford.edu/downloads/classifier.shtml
http://maxent.sourceforge.net
第五讲结束!
附:课程及课件pdf下载MIT英文网页地址:
http://people.csail.mit.edu/regina/6881/
注:本文遵照麻省理工学院开放式课程创作共享规范翻译发布,转载请注明出处“我爱自然语言处理”:www.52nlp.cn
本文链接地址:https://www.52nlp.cn/mit-nlp-fifth-lesson-maximum-entropy-and-log-linear-models-fifth-part/