HMM学习最佳范例三：隐藏模式

三、隐藏模式（Hidden Patterns）

1、马尔科夫过程的局限性
　　在某些情况下，我们希望找到的模式用马尔科夫过程描述还显得不充分。回顾一下天气那个例子，一个隐士也许不能够直接获取到天气的观察情况，但是他有一些水藻。民间传说告诉我们水藻的状态与天气状态有一定的概率关系——天气和水藻的状态是紧密相关的。在这个例子中我们有两组状态，观察的状态（水藻的状态）和隐藏的状态（天气的状态）。我们希望为隐士设计一种算法，在不能够直接观察天气的情况下，通过水藻和马尔科夫假设来预测天气。
　　一个更实际的问题是语音识别，我们听到的声音是来自于声带、喉咙大小、舌头位置以及其他一些东西的组合结果。所有这些因素相互作用产生一个单词的声音，一套语音识别系统检测的声音就是来自于个人发音时身体内部物理变化所引起的不断改变的声音。
　　一些语音识别装置工作的原理是将内部的语音产出看作是隐藏的状态，而将声音结果作为一系列观察的状态，这些由语音过程生成并且最好的近似了实际（隐藏）的状态。在这两个例子中，需要着重指出的是，隐藏状态的数目与观察状态的数目可以是不同的。一个包含三个状态的天气系统（晴天、多云、雨天）中，可以观察到4个等级的海藻湿润情况（干、稍干、潮湿、湿润）；纯粹的语音可以由80个音素描述，而身体的发音系统会产生出不同数目的声音，或者比80多，或者比80少。
　　在这种情况下，观察到的状态序列与隐藏过程有一定的概率关系。我们使用隐马尔科夫模型对这样的过程建模，这个模型包含了一个底层隐藏的随时间改变的马尔科夫过程，以及一个与隐藏状态某种程度相关的可观察到的状态集合。

2、隐马尔科夫模型（Hidden Markov Models）
　　下图显示的是天气例子中的隐藏状态和观察状态。假设隐藏状态（实际的天气）由一个简单的一阶马尔科夫过程描述，那么它们之间都相互连接。
　　
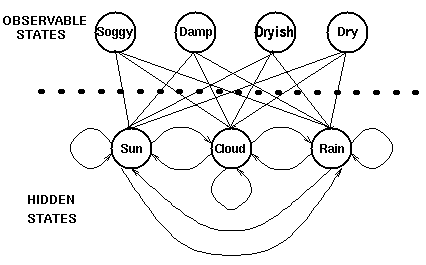
　　隐藏状态和观察状态之间的连接表示：在给定的马尔科夫过程中，一个特定的隐藏状态生成特定的观察状态的概率。这很清晰的表示了‘进入’一个观察状态的所有概率之和为1，在上面这个例子中就是Pr(Obs|Sun)，Pr(Obs|Cloud) 及 Pr(Obs|Rain)之和。这里再引用一下读者jiuren的注解：

这里作者是把obs作为参数来用，是说Sum_{Obs=Dry,Dryish,Damp,Soggy}(Obs|Sun) = 1;
Sum_{Obs=Dry,Dryish,Damp,Soggy}(Obs|Cloud) = 1;
Sum_{Obs=Dry,Dryish,Damp,Soggy}(Obs|Rain) = 1;

　　除了定义了马尔科夫过程的概率关系，我们还有另一个矩阵，定义为混淆矩阵（confusion matrix），它包含了给定一个隐藏状态后得到的观察状态的概率。对于天气例子，混淆矩阵是：
　　
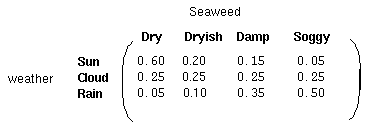
　　注意矩阵的每一行之和是1。

3、总结（Summary）
　　我们已经看到在一些过程中一个观察序列与一个底层马尔科夫过程是概率相关的。在这些例子中，观察状态的数目可以和隐藏状态的数码不同。
　　我们使用一个隐马尔科夫模型（HMM）对这些例子建模。这个模型包含两组状态集合和三组概率集合：
　　* 隐藏状态：一个系统的（真实）状态，可以由一个马尔科夫过程进行描述（例如，天气）。
　　* 观察状态：在这个过程中‘可视’的状态（例如，海藻的湿度）。
　　* pi向量：包含了（隐）模型在时间t=1时一个特殊的隐藏状态的概率（初始概率）。
　　* 状态转移矩阵：包含了一个隐藏状态到另一个隐藏状态的概率
　　* 混淆矩阵：包含了给定隐马尔科夫模型的某一个特殊的隐藏状态，观察到的某个观察状态的概率。
　　因此一个隐马尔科夫模型是在一个标准的马尔科夫过程中引入一组观察状态，以及其与隐藏状态间的一些概率关系。

未完待续：隐马尔科夫模型

本文翻译自：http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html
部分翻译参考：隐马尔科夫模型HMM自学

转载请注明出处“我爱自然语言处理”：www.52nlp.cn

本文链接地址：https://www.52nlp.cn/hmm-learn-best-practices-three-hidden-patterns