HMM学习最佳范例六：维特比算法2

六、维特比算法（Viterbi Algorithm）

寻找最可能的隐藏状态序列(Finding most probable sequence of hidden states)

2b.计算t=1时刻的局部概率's
　　我们计算的局部概率是作为最可能到达我们当前位置的路径的概率（已知的特殊知识如观察概率及前一个状态的概率）。当t=1的时候，到达某状态的最可能路径明显是不存在的；但是，我们使用t=1时的所处状态的初始概率及相应的观察状态k1的观察概率计算局部概率；即
　　　　　　　　　　
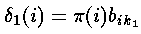
　　——与前向算法类似，这个结果是通过初始概率和相应的观察概率相乘得出的。

2c.计算t>1时刻的局部概率's
　　现在我们来展示如何利用t-1时刻的局部概率计算t时刻的局部概率。
　　考虑如下的网格：
　　　　
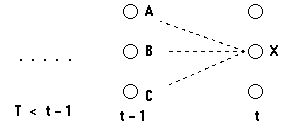
　　我们考虑计算t时刻到达状态X的最可能的路径；这条到达状态X的路径将通过t-1时刻的状态A，B或C中的某一个。
　　因此，最可能的到达状态X的路径将是下面这些路径的某一个
　　　　　　　（状态序列），...，A，X
　　　　　　　（状态序列），...，B，X
或　　　　　　（状态序列），...，C，X
　　我们想找到路径末端是AX,BX或CX并且拥有最大概率的路径。
　　回顾一下马尔科夫假设：给定一个状态序列，一个状态发生的概率只依赖于前n个状态。特别地，在一阶马尔可夫假设下，状态X在一个状态序列后发生的概率只取决于之前的一个状态，即
　　　Pr (到达状态A最可能的路径) .Pr (X | A) . Pr (观察状态 | X)
　　与此相同，路径末端是AX的最可能的路径将是到达A的最可能路径再紧跟X。相似地，这条路径的概率将是：
　　　Pr (到达状态A最可能的路径) .Pr (X | A) . Pr (观察状态 | X)
　　因此，到达状态X的最可能路径概率是：
　　
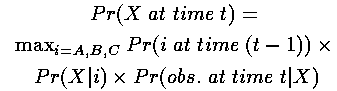
　　其中第一项是t-1时刻的局部概率，第二项是状态转移概率以及第三项是观察概率。
　　泛化上述公式，就是在t时刻，观察状态是kt，到达隐藏状态i的最佳局部路径的概率是：
　　　　　
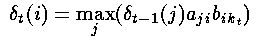
　　这里，我们假设前一个状态的知识（局部概率）是已知的，同时利用了状态转移概率和相应的观察概率之积。然后，我们就可以在其中选择最大的概率了（局部概率）。

未完待续：维特比算法3

本文翻译自：http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html
部分翻译参考：隐马尔科夫模型HMM自学

转载请注明出处“我爱自然语言处理”：www.52nlp.cn

本文链接地址：https://www.52nlp.cn/hmm-learn-best-practices-six-viterbi-algorithm-2