
六、维特比算法(Viterbi Algorithm)
寻找最可能的隐藏状态序列(Finding most probable sequence of hidden states)
对于一个特殊的隐马尔科夫模型(HMM)及一个相应的观察序列,我们常常希望能找到生成此序列最可能的隐藏状态序列。
1.穷举搜索
我们使用下面这张网格图片来形象化的说明隐藏状态和观察状态之间的关系:
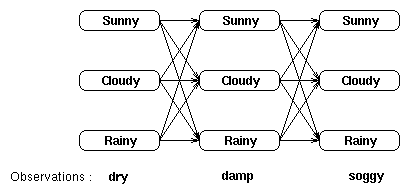
我们可以通过列出所有可能的隐藏状态序列并且计算对于每个组合相应的观察序列的概率来找到最可能的隐藏状态序列。最可能的隐藏状态序列是使下面这个概率最大的组合:
Pr(观察序列|隐藏状态的组合)
例如,对于网格中所显示的观察序列,最可能的隐藏状态序列是下面这些概率中最大概率所对应的那个隐藏状态序列:
Pr(dry,damp,soggy | sunny,sunny,sunny), Pr(dry,damp,soggy | sunny,sunny,cloudy), Pr(dry,damp,soggy | sunny,sunny,rainy), . . . . Pr(dry,damp,soggy | rainy,rainy,rainy)
这种方法是可行的,但是通过穷举计算每一个组合的概率找到最可能的序列是极为昂贵的。与前向算法类似,我们可以利用这些概率的时间不变性来降低计算复杂度。
2.使用递归降低复杂度
给定一个观察序列和一个隐马尔科夫模型(HMM),我们将考虑递归地寻找最有可能的隐藏状态序列。我们首先定义局部概率 ,它是到达网格中的某个特殊的中间状态时的概率。然后,我们将介绍如何在t=1和t=n(>1)时计算这些局部概率。
,它是到达网格中的某个特殊的中间状态时的概率。然后,我们将介绍如何在t=1和t=n(>1)时计算这些局部概率。
这些局部概率与前向算法中所计算的局部概率是不同的,因为它们表示的是时刻t时到达某个状态最可能的路径的概率,而不是所有路径概率的总和。
2a.局部概率 's和局部最佳途径
's和局部最佳途径
考虑下面这个网格,它显示的是天气状态及对于观察序列干燥,湿润及湿透的一阶状态转移情况:
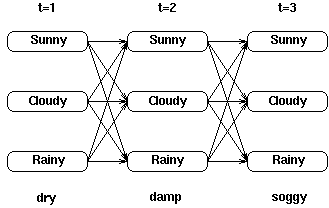
对于网格中的每一个中间及终止状态,都有一个到达该状态的最可能路径。举例来说,在t=3时刻的3个状态中的每一个都有一个到达此状态的最可能路径,或许是这样的:
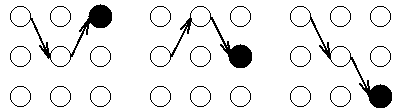
我们称这些路径局部最佳路径(partial best paths)。其中每个局部最佳路径都有一个相关联的概率,即局部概率或 。与前向算法中的局部概率不同,
。与前向算法中的局部概率不同, 是到达该状态(最可能)的一条路径的概率。
是到达该状态(最可能)的一条路径的概率。
因而 (i,t)是t时刻到达状态i的所有序列概率中最大的概率,而局部最佳路径是得到此最大概率的隐藏状态序列。对于每一个可能的i和t值来说,这一类概率(及局部路径)均存在。
(i,t)是t时刻到达状态i的所有序列概率中最大的概率,而局部最佳路径是得到此最大概率的隐藏状态序列。对于每一个可能的i和t值来说,这一类概率(及局部路径)均存在。
特别地,在t=T时每一个状态都有一个局部概率和一个局部最佳路径。这样我们就可以通过选择此时刻包含最大局部概率的状态及其相应的局部最佳路径来确定全局最佳路径(最佳隐藏状态序列)。
未完待续:维特比算法2
本文翻译自:http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html
部分翻译参考:隐马尔科夫模型HMM自学
转载请注明出处“我爱自然语言处理”:www.52nlp.cn
本文链接地址:https://www.52nlp.cn/hmm-learn-best-practices-six-viterbi-algorithm-1
好像没有关于训练算法baum welch的
[回复]
admin 回复:
14 8 月, 2009 at 21:36
请耐心等待,后继我会继续写这个系列,可以先看看几篇关于HMM的经典论文:
An Introduction to Hidden Markov Models;
A tutorial on Hidden Markov Models and selected applications in speech recognition;
[回复]
谢谢您的工作!
[回复]
admin 回复:
23 8 月, 2009 at 19:38
不用客气,欢迎常来!
[回复]
<>书中也有介绍HMM:
http://www.douban.com/subject/4114152/
希望对初学者有帮助。
[回复]
52nlp 回复:
9 1 月, 2010 at 19:22
谢谢!
[回复]
楼主很强大,谢谢您的工作……
[回复]
52nlp 回复:
22 1 月, 2010 at 20:53
不客气,欢迎常来看看!
[回复]
lz,您说“最可能的隐藏状态序列是使下面这个概率最大的组合:
Pr(观察序列|隐藏状态的组合)”
那为什么不是“Pr(隐藏状态的组合|观察序列)”呢
[回复]
52nlp 回复:
21 4 月, 2010 at 23:32
首先,这个不是我说的,而是翻译而来的。事实上,终极目标是求“Pr(隐藏状态的组合|观察序列)”的最大值。但是如何求解这个公式你是否考虑过?
可以看一下关于HMM的经典论文:A tutorial on Hidden Markov Models and selected applications in speech recognition,在其“B.Solution to Problem 2”,对于维特比算法的由来做了一点解释,关于HMM的基本问题2,可以有多种优化目标的界定。对于你的这个问题,做了一点说明:to maximize P(Q|O,h)等价于P(Q,O|h),这里h是已知的HMM隐马尔科夫模型。
[回复]
想问一下 我做一个根据五个特征(也就是一个事物的五个属性)预测一个值
具体是药物的生物利用度,已知五个属性
这个模型中 观察序列是什么 状态怎么定
很困惑
[回复]
52nlp 回复:
13 5 月, 2010 at 23:49
抱歉,不太明白你所描述的这个问题,最好能将问题本身描述得再清楚一点,才能判断是否可以利用HMM解决这个问题。
[回复]
hydliuliu 回复:
17 5 月, 2010 at 09:16
是药物的生物利用度跟以下5个特征相关
下面是数据的列表
一 二 三 四 五 生物利用度
18.6 67 52 8 6.5 高
19.2 63 75 12.5 8.21 高
12 49 38 18.5 6.34 低
21.6 57 25 10.2 6.5 高
15.2 70 38.9 12.5 6.8 低
12 49 38 21.5 6.34 低
这是部分的列表 还有一系列5个特征的数据 想利用HMM预测出生物利用度的高低
[回复]
52nlp 回复:
18 5 月, 2010 at 00:08
感觉这个问题利用HMM处理并不是一个好的选择,HMM更适合一些序列标记的问题,所以首先一个问题是:这5个特征直接是否有联系?如果有联系,要处理的一个问题是计算它们直接的一些关系。
这个应该属于二元分类的问题,可以考虑利用一些判别模型的方法来解决,例如最大熵模型或者SVM,这样重点关注的地方就是训练这几个特征的权重了,可以使用一些开源工具来训练。
hydliuliu 回复:
18 5 月, 2010 at 08:32
非常感谢 这个我用SVM做过了 想做个算法比较
你这个系列的文档我都看完了 还是找不到头绪
52nlp 回复:
18 5 月, 2010 at 23:29
不客气,感觉你找不到头绪的原因在于这个问题用HMM来解决不对路。
正在学习这个,我想把关于HMMs这几篇转载到我自己的qq空间了,可否
[回复]
52nlp 回复:
19 11 月, 2010 at 21:35
没问题。
[回复]
Mark 回复:
22 6 月, 2013 at 09:16
局部概率β‘s 后面的‘s 到底是什么意思?
[回复]
[...] 对于问题2,怎么最好地解释观测序列?可以认为该问题是译码过程,即需要最大化将被正确猜测的状态的期望数目。译码最常用的方法是Viterbi算法,因为它能够有效地计算最可能地状态序列。Viterbi算法地详细过程参见:HMM学习最佳范例六:维特比算法。 [...]
[...] 对于问题2,怎么最好地解释观测序列?可以认为该问题是译码过程,即需要最大化将被正确猜测的状态的期望数目。译码最常用的方法是Viterbi算法,因为它能够有效地计算最可能地状态序列。Viterbi算法地详细过程参见:HMM学习最佳范例六:维特比算法。 [...]
局部概率β‘s 后面的‘s 到底是什么意思?
[回复]
有关于部队运用HMM模型以及viterbi算法的实例吗?急
求帮
[回复]
52nlp 回复:
15 4 月, 2016 at 11:07
抱歉,没有
[回复]
谢谢博主*—*
[回复]
你好,博主,如果用HMM来进行人脸识别,有没有源码呢?
[回复]
52nlp 回复:
25 7 月, 2016 at 22:45
不太清楚,自己google吧
[回复]
火焰 回复:
26 7 月, 2016 at 09:30
不好意思,再问一下,人脸的HMM的 观测序列是什么,是人脸特征值吗
[回复]
52nlp 回复:
26 7 月, 2016 at 20:05
抱歉,不熟悉人脸识别