七、前向-后向算法(Forward-backward algorithm)
上一节我们定义了两个变量及相应的期望值，本节我们利用这两个变量及其期望值来重新估计隐马尔科夫模型（HMM）的参数
如果我们定义当前的HMM模型为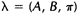
，那么可以利用该模型计算上面三个式子的右端；我们再定义重新估计的HMM模型为
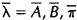，那么上面三个式子的左端就是重估的HMM模型参数。Baum及他的同事在70年代证明了
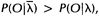因此如果我们迭代地的计算上面三个式子，由此不断地重新估计HMM的参数，那么在多次迭代后可以得到的HMM模型的一个最大似然估计。不过需要注意的是，前向-后向算法所得的这个结果（最大似然估计）是一个局部最优解。
关于前向-后向算法和EM算法的具体关系的解释，大家可以参考HMM经典论文《A tutorial on Hidden Markov Models and selected applications in speech recognition》，这里就不详述了。下面我们给出UMDHMM中的前向-后向算法示例，这个算法比较复杂，这里只取主函数，其中所引用的函数大家如果感兴趣的话可以自行参考UMDHMM。
前向-后向算法程序示例如下（在baum.c中):
void BaumWelch(HMM *phmm, int T, int *O, double **alpha, double **beta, double **gamma, int *pniter, double *plogprobinit, double *plogprobfinal)
{
int i, j, k;
int t, l = 0;
double logprobf, logprobb, threshold;
double numeratorA, denominatorA;
double numeratorB, denominatorB;
double ***xi, *scale;
double delta, deltaprev, logprobprev;
deltaprev = 10e-70;
xi = AllocXi(T, phmm->N);
scale = dvector(1, T);
ForwardWithScale(phmm, T, O, alpha, scale, &logprobf);
*plogprobinit = logprobf; /* log P(O |intial model) */
BackwardWithScale(phmm, T, O, beta, scale, &logprobb);
ComputeGamma(phmm, T, alpha, beta, gamma);
ComputeXi(phmm, T, O, alpha, beta, xi);
logprobprev = logprobf;
do
{
/* reestimate frequency of state i in time t=1 */
for (i = 1; i <= phmm->N; i++)
phmm->pi[i] = .001 + .999*gamma[1][i];
/* reestimate transition matrix and symbol prob in
each state */
for (i = 1; i <= phmm->N; i++)
{
denominatorA = 0.0;
for (t = 1; t <= T - 1; t++)
denominatorA += gamma[t][i];
for (j = 1; j <= phmm->N; j++)
{
numeratorA = 0.0;
for (t = 1; t <= T - 1; t++)
numeratorA += xi[t][i][j];
phmm->A[i][j] = .001 +
.999*numeratorA/denominatorA;
}
denominatorB = denominatorA + gamma[T][i];
for (k = 1; k <= phmm->M; k++)
{
numeratorB = 0.0;
for (t = 1; t <= T; t++)
{
if (O[t] == k)
numeratorB += gamma[t][i];
}
phmm->B[i][k] = .001 +
.999*numeratorB/denominatorB;
}
}
ForwardWithScale(phmm, T, O, alpha, scale, &logprobf);
BackwardWithScale(phmm, T, O, beta, scale, &logprobb);
ComputeGamma(phmm, T, alpha, beta, gamma);
ComputeXi(phmm, T, O, alpha, beta, xi);
/* compute difference between log probability of
two iterations */
delta = logprobf - logprobprev;
logprobprev = logprobf;
l++;
}
while (delta > DELTA); /* if log probability does not
change much, exit */
*pniter = l;
*plogprobfinal = logprobf; /* log P(O|estimated model) */
FreeXi(xi, T, phmm->N);
free_dvector(scale, 1, T);
}
前向-后向算法就到此为止了。
未完待续：总结
注：原创文章，转载请注明出处“我爱自然语言处理”：www.52nlp.cn
本文链接地址：https://www.52nlp.cn/hmm-learn-best-practices-seven-forward-backward-algorithm-5
很是好啊,谢谢楼主的分享,
[回复]
欢迎常来看看！
[回复]
楼主，你好。用Baum-welch算法来训练HMM模型时，只用输入隐藏状态的个数，观察向量的个数，观察序列，我有个几个疑问：
1.单单靠这些，怎么来评估这个参数模型就是最优的？因为我用这个算法测试的时候，每次迭代次说都是1.
2.
现在我想利用HMM来做人体行为识别，我有一个基本行为库，其中包括三个行为（也就是隐藏状态）：walk，run，jump；库中包括的是人体不同行为的轮廓，每个行为对应8个观察向量，也就是说此模型总共观察向量有32个。我该怎么训练HMM呢
[回复]
52nlp 回复:
1 12 月, 2009 at 21:10
不好意思，晚上回来的比较迟。
首先用Baum-welch算法来训练HMM模型本身得到的解是局部最优，而全局最优解。另外，只给出这几个条件用这个算法进行无监督训练的HMM模型效果应该很差。
举个例子，在实际的词性标注应用中，也会辅之以词典词性信息或者词类信息才能得到一个相对较好的HMM词性标注模型。但就是这样，也没有从一个已经做好标注的小语料库中直接得到的HMM模型的准确率高。
所以对于你的第2个问题，最好的方法是你能建立一个与实际问题相对应的训练集，譬如：
O1/walk O2/jump O3/run O4/run ...
....
其中Oi是观察向量，从这样的训练集中直接计算生成一个HMM模型的效果估计会比利用Baum-welch算法来训练HMM模型好很多。
[回复]
jumay 回复:
1 12 月, 2009 at 21:26
谢谢你！O(∩_∩)O~ 我再考虑一下
[回复]
你好，楼主，我有一个问题：用上述bw算法来训练HMM的时候，按理说迭代次数是不同的，但是不管我的输入观察序列是多少，迭代次数都是1.为什么会这样
[回复]
52nlp 回复:
1 12 月, 2009 at 21:16
没有仔细考虑这个问题，估计输入序列可能过短，可以试着用100长以上的序列试一下。不太清楚原因，在我讲的《HMM在自然语言处理中的应用一：词性标注3》中训练序列的长度是590。
另外，觉得在umdhmm中直接使用Baum-welch算法来训练HMM模型只适用于教学举例，真正的应用中如果没有很好的训练集也应该辅之以一些辅助信息。
[回复]
jumay 回复:
1 12 月, 2009 at 21:54
你好！谢谢你的答复。这个地方还是不太理解，即便是我辅助的有观察值对应的隐藏状态，比如说0/walk 2/walk 3/walk 8/run 9/run 10/run ，该怎么利用这些参数和bw算法进行有监督的训练呢
[回复]
52nlp 回复:
1 12 月, 2009 at 22:59
这个可以参考“HMM在自然语言处理中的应用一：词性标注5”，直接计算HMM的各个参数值就可了。
博主，我一直没看懂baum-welch算法，即使是看着umdhmm的代码，博主提到的《A tutorial on Hidden Markov Models and selected applications in speech recognition》，是L.R.Rabiner的那一篇吗？
我想应用hmm识别到图像匹配中去，训练时效果很差，所以想仔细理解一下训练用的算法。
[回复]
52nlp 回复:
10 10 月, 2010 at 00:10
是这一篇论文，建议好好读读英文原始文献，我这里翻译的比较粗糙。
另外除了多花一点时间琢磨这个算法外，所需要的一些基本数学知识也要了解一下。
[回复]
博主你好，我有几个问题想向你请教，希望你给予指点，先谢谢了。
1.我现在在做中文语料的词性标注，首先要用EM算法来估计AB矩阵，
所以我要用到前后向算法，但是一次前后向算法之后，得到的两个前后向矩阵
均溢出！（前后向算法就会溢出）；
2.关于EM算法初始值的选择，我怎样才能尽可能选择好的初始值呢？
[回复]
Beingspider 回复:
24 12 月, 2010 at 21:58
第一个问题已经解决，我找了资料第二个问题主要是对B(发射概率)的初始化。博主有没有好的建议？或者能给我提供些关于K均值分割算法的资料，谢谢了。
[回复]
52nlp 回复:
24 12 月, 2010 at 23:05
非常抱歉，这方面我没有什么经验，也没有这方面的资料！
[回复]
Beingspider 回复:
25 12 月, 2010 at 10:51
呵呵，没事。还是要谢谢你。
在前向算法与后向算法中都分别有带WithScale的函数；比如在backward.c 中有两个函数，一个是Backward()一个是BackwardWithScale()，请问后者有什么用。本人比较菜，望博主能指点一二。谢谢
[回复]
52nlp 回复:
10 4 月, 2011 at 17:50
从代码中看scale一个比例因子数组，它是对前向算法和后向算法每一轮的中间结果进行按比例修正的，至于为什么这样做，我也不是很清楚，抱歉！
[回复]
请问WithScale是什么意思，有什么用 回复:
10 4 月, 2011 at 20:55
Thank you anyway
[回复]
chen 回复:
5 12 月, 2013 at 11:33
这个问题是这样： C语言中的double类型的阶码只有11位，当O序列过长，算出的概率值是很小的，比如当概率值为
2^-3000，这个pprob会被当成0,log(pprob)会被当成-INF。但实际上log(pprob)是-3000才对，而-3000是个很普通，可以正常表示的数。
故：withscal方法再算log(pprob)时，绕过了计算pprob，再log的过程，而是直接计算了，这样就不至于当O序列过长时，得到一些无意义的数了，基本原理是log(a/b)=log(a)-log(b)
chen 回复:
5 12 月, 2013 at 11:40
所以当O序列过长时，用带withscal的方法，否则pprob都是0,log(pprob)都是-INF。log一个数，往往是为了缩放，log函数是单调的，并不影响两个数的相对大小，即如果a<b,则一定有：log(a)<log(b), 这种缩放很常见的。
如果不理解，不要纠结了，withscal的结果就是概率值取log的结果，没问题。
此代码在模型参数调整中存在错误。我在改写的C#代码里修正了此错误。
详见：http://blog.csdn.net/jhqin/archive/2011/06/09/6534916.aspx
[回复]
52nlp 回复:
10 6 月, 2011 at 13:08
谢谢指正！
[回复]
我想问一下 看到一书上提到用前向后向算法训练HMM时，HMM应用的典型场合是可以得到词典。这句话可以理解成只有语料（词汇，比如msr_training.txt分好词的文本）么？还有一个问题是HMM的初始化，应该是什么呢
[回复]
您好，请教您一个问题：在给定观察序列O的情况下，用B-W算法寻求一个λ使得P(O|λ)最大，这里的P(O|λ)与用迭代好了的λ使用前向算法计算的P(O|λ)是一致的吗？
[回复]
52nlp 回复:
1 8 月, 2012 at 20:31
应该是一致的吧，看你使用的目的了。
[回复]
袁军 回复:
1 8 月, 2012 at 21:42
用在不同的地方会不一致吗，还请博主举个例子比方说？ 谢谢！
[回复]
52nlp 回复:
3 8 月, 2012 at 15:26
我理解你的这个问题中前者是求参，后者是应用，不冲突的
博主您好，我想请教您一个问题，请问在baum-welch算法中对参数进行重估时，B的重估的含义是什么呢？
[回复]
[…] 隐马尔科夫模型(Hidden Markov Model),它是一种统计学模型，用来描述随机事件的发生。该模型与马尔科夫模型的差别在于它的状态是隐含的，我们看到的是事件的发生。隐状态之间有转换概率，从隐状态到事件之间有映射概率。 2 HMM模型能够干什么？ 三个问题： 1）给出HMM模型和观测序列，计算在该模型下得到该观测序列的概率 2）给出HMM模型和观测序列，计算在该模型下得到该观测序列最有可能的隐状态序列 3）给定观测序列，估计HMM模型 3 对于每个问题的解答以及例子 对于问题1，一般采用的是forward algorithm(也可以用backward algorithm)。该算法的实现如下（Perl语言）： #指定HMM模型的参数 my $stateNum=3; my $obsNum=10; my @initialP=qw(0.1 0.5 0.4); my @state=qw(A B C); my @obsKind=qw(1 2 3 4); my $obsKind2num; for(my i=0;i<scalar @obsKind;$i++){ obsKind2num−>$obsKind[$i]=i; } my @Atransition=(0.8,0.1,0.1); my @Btransition=(0.2,0.6,0.2); my @Ctransition=(0.3,0.1,0.6); my $transitionRef->{‘A’}=@Atransition; $transitionRef->{‘B’}=@Btransition; $transitionRef->{‘C’}=@Ctransition; my @Atransmit=(0.1,0.2,0.3,0.4); my @Btransmit=(0.2,0.1,0.2,0.5); my @Ctransmit=(0.3,0.4,0.1,0.2); my $transmitRef->{‘A’}=@Atransmit; $transmitRef->{‘B’}=@Btransmit; $transmitRef->{‘C’}=@Ctransmit; my @obs=qw(1 4 2 3 1 4 1 1 4 3); my $proRef; #前向向量 for(my i=0;i<scalar @obs;$i++){ my obsKindNum=obsKind2num->{obs[i]}; if($i ==0){ for(my i=0;i<scalar @state;$i++){ proRef−>0−>$state[$i]=initialP[i]∗transmitRef->{state[i]}->[$obsKindNum]; } next; } for(my k=0;k<scalar @state;$k++){ my $pro=0; for(my h=0;h<scalar @state;$h++){ pro+=proRef->{i-1}->{$state[$h]}*transitionRef->{state[h]}->[$k]; } proRef−>$i−>$state[$k]=pro*transmitRef−>$state[$k]−>[obsKindNum]; } } #把T时刻各个状态的概率相加得到观测序列的概率 my $proFinal=0; foreach my$state(@state){ proFinal+=proRef->{(scalar @obs-1)}->{$state}; } print “The final probability is: “,$proFinal,”n”; 对于问题2,同样是forward algorithm和backword algorithm都可以用。forward algorithm的实现如下： #指定HMM模型的参数 my $stateNum=3; my $obsNum=10; my @initialP=qw(0.1 0.5 0.4); my @state=qw(A B C); my @obsKind=qw(1 2 3 4); my $obsKind2num; for(my i=0;i<scalar @obsKind;$i++){ obsKind2num−>$obsKind[$i]=i; } my @Atransition=(0.8,0.1,0.1); my @Btransition=(0.2,0.6,0.2); my @Ctransition=(0.3,0.1,0.6); my $transitionRef->{‘A’}=@Atransition; $transitionRef->{‘B’}=@Btransition; $transitionRef->{‘C’}=@Ctransition; my @Atransmit=(0.1,0.2,0.3,0.4); my @Btransmit=(0.2,0.1,0.2,0.5); my @Ctransmit=(0.3,0.4,0.1,0.2); my $transmitRef->{‘A’}=@Atransmit; $transmitRef->{‘B’}=@Btransmit; $transmitRef->{‘C’}=@Ctransmit; my @obs=qw(1 1 4 2 2 3 3); my $current2preMax; #用来回溯状态序列 my proRef; #proRef->{index}->{state} 前向向量 for(my index=0;index <scalar @obs;$index++){ my obsNum=obsKind2num->{obs[index]}; my currentObs=obs[$index]; if($index==0){ for(my i=0;i<scalar @state;$i++){ proRef−>$index−>$state[$i]=initialP[i]∗transmitRef->{state[i]}->[$obsNum]; } next; } for(my i=0;i<scalar @state;$i++){ my $subRef; for(my j=0;j<scalar @state;$j++){ subRef−>$state[$j]=proRef->{index-1}->{$state[$j]}*transitionRef->{state[j]}->[$i]; } my @previousState=sort {subRef−>$b<=>subRef->{a}}keys %{subRef}; proRef−>$index−>$state[$i]=subRef->{previousState[0]}*transmitRef->{state[i]}->[$obsNum]; current2preMax−>$index−>$state[$i]=previousState[0]; } } my @index=sort {b<=>a}keys %{$current2preMax}; my @finalStateSort=sort {proRef−>$index[0]−>$b<=>proRef->{index[0]}->{a}}keys %{proRef->{index[0]}}; print “The final step: “,index[0],”tthestatewiththelargestprobiligy:”,finalStateSort[0],”n”; #回溯过程 my @stateSeq; my finalState=finalStateSort[0]; push(@stateSeq,$finalState); for(my i=index[0];i>0;i–){ my cur=stateSeq[-1]; my next=current2preMax->{i}->{cur}; push(@stateSeq,$next); } @stateSeq=reverse @stateSeq; print join(“-”,@stateSeq),”n”; print join(“-”,@obs),”n”; 对于问题3，采用forward-backward algorithm，也称为 Baum-Welch算法。它是一种贪婪算法，往往只能够达到局部最优。它的实现如下： ######################################################################### #采用Forward-backward algorithm （Baum-Welch算法）估计HMM模型的参数； ######################################################################### #模型参数的初始化 my $stateNum=3; my $obsNum=10; my @initialP=qw(0.1 0.5 0.4); my @state=qw(A B C); my @obsKind=qw(1 2 3 4); my $obsKind2num; for(my i=0;i<scalar @obsKind;$i++){ obsKind2num−>$obsKind[$i]=i; } my @Atransition=(0.8,0.1,0.1); my @Btransition=(0.2,0.6,0.2); my @Ctransition=(0.3,0.1,0.6); my $transitionRef->{‘A’}=@Atransition; $transitionRef->{‘B’}=@Btransition; $transitionRef->{‘C’}=@Ctransition; my @Atransmit=(0.1,0.2,0.3,0.4); my @Btransmit=(0.2,0.1,0.2,0.5); my @Ctransmit=(0.3,0.4,0.1,0.2); my $transmitRef->{‘A’}=@Atransmit; $transmitRef->{‘B’}=@Btransmit; $transmitRef->{‘C’}=@Ctransmit; my @obs=qw(1 1 4 1 2 1 1 2 3 4 2 2 3 3 4 2); #观测序列 #初始模型下得到观测序列的概率; my $proBefore=0; my $proRef; for(my i=0;i<scalar @obs;$i++){ my obsKindNum=obsKind2num->{obs[i]}; if($i ==0){ for(my i=0;i<scalar @state;$i++){ proRef−>0−>$state[$i]=initialP[i]∗transmitRef->{state[i]}->[$obsKindNum]; } next; } for(my k=0;k<scalar @state;$k++){ my $pro=0; for(my h=0;h<scalar @state;$h++){ pro+=proRef->{i-1}->{$state[$h]}*transitionRef->{state[h]}->[$k]; } proRef−>$i−>$state[$k]=pro*transmitRef−>$state[$k]−>[obsKindNum]; } } foreach mystate(keysproRef->{(scalar @obs)-1}}){ proBefore+=proRef->{(scalar @obs)-1}->{$state}; } proBefore=log(proBefore); open(OUT,”>test”)or die”$!”; my proAfter=proBefore; my $threshold=1e-10; #判断迭代过程终止的cutoff for(my time=1;time < 1000;$time++){ my epsonRef; #epsonRef->{t}->{i}->{$j} my alphaRef; #alphaRef->{t}->{i} my betaRef; #betaRef->{t}->{i} #calculate $alphaRef; for(my t=0;t <scalar @obs;$t++){ my obsKindNum=obsKind2num->{obs[t]}; if($t==0){ for(my i=0;i<scalar @state;$i++){ alphaRef−>0−>$state[$i]=initialP[i]∗transmitRef->{state[i]}->[$obsKindNum]; } next; } for(my i=0;i<scalar @state;$i++){ my $pro=0; for(my j=0;j<scalar @state;$j++){ pro+=alphaRef->{t-1}->{$state[$j]}*transitionRef->{state[j]}->[$i]; } alphaRef−>$t−>$state[$i]=pro*transmitRef−>$state[$i]−>[obsKindNum]; } } #calculate $betaRef; for(my t=(scalar@obs−1);t >=0;$t–){ if($t==((scalar @obs)-1)){ for(my i=0;i<scalar @state;$i++){ betaRef->{t}->{state[i]}=1; } next; } my obsKindNum=obsKind2num->{obs[t+1]}; for(my i=0;i<scalar @state;$i++){ my $pro=0; for(my j=0;j<scalar @state;$j++){ pro+=betaRef->{t+1}->{$state[$j]}*transitionRef->{state[i]}->[j]∗transmitRef->{state[j]}->[$obsKindNum]; } betaRef−>$t−>$state[$i]=pro; } } #calculate $epsonRef; for(my t=0;t <scalar @obs-1;$t++){ my obsKindNum=obsKind2num->{obs[t+1]}; my $denominator=0; for(my i=0;i<scalar @state;$i++){ for(my j=0;j<scalar @state;$j++){ denominator+=alphaRef->{t}->{$state[$i]}*transitionRef->{state[i]}->[j]∗transmitRef->{state[j]}->[obsKindNum]∗betaRef->{t+1}->{state[$j]}; } } for(my i=0;i<scalar @state;$i++){ for(my j=0;j<scalar @state;$j++){ my $numerator=0; numerator+=alphaRef->{t}->{$state[$i]}*transitionRef->{state[i]}->[j]∗transmitRef->{state[j]}->[obsKindNum]∗betaRef->{t+1}->{state[$j]}; epsonRef−>$t−>$state[$i]−>$state[$j]=numerator/$denominator; } } } #calculate $rRef; my $rRef; for(my t=0;t<scalar @obs;$t++){ for(my i=0;i<scalar @state;$i++){ my $r=0; foreach mystate(keysepsonRef->{t}->{state[$i]}}){ r+=epsonRef->{t}->{state[i]}->{state}; } rRef−>$t−>$state[$i]=r; } } #Re-estimation of the parameters; for(my i=0;i<scalar @state;$i++){ initialP[i]=rRef->{0}->{state[$i]}; } for(my i=0;i<scalar @state;$i++){ my $denominator=0; for(my t=0;t<(scalar @obs)-1;$t++){ denominator+=rRef->{t}->{state[$i]}; } for(my j=0;j<scalar @state;$j++){ my $numerator=0; for(my t=0;t < (scalar @obs)-1;$t++){ numerator+=epsonRef->{t}->{state[$i]} ->{state[j]}; } transitionRef−>$state[$i]−>[j]=numerator/denominator; } } for(my i=0;i<scalar @state;$i++){ my $denominator=0; for(my t=0;t<(scalar @obs);$t++){ denominator+=rRef->{t}->{state[$i]}; } for(my j=0;j<scalar @obsKind;$j++){ my $numerator=0; for(my t=0;t<scalar @obs;$t++){ if(obs[t]==obsKind[j]){ numerator+=rRef->{t}->{state[$i]}; } } transmitRef−>$state[$i]−>[j]=numerator/denominator; } } #计算更新参数后的HMM模型得到观测序列的概率； my $proRef; $proAfter=0; for(my i=0;i<scalar @obs;$i++){ my obsKindNum=obsKind2num->{obs[i]}; if($i ==0){ for(my i=0;i<scalar @state;$i++){ proRef−>0−>$state[$i]=initialP[i]∗transmitRef->{state[i]}->[$obsKindNum]; } next; } for(my k=0;k<scalar @state;$k++){ my $pro=0; for(my h=0;h<scalar @state;$h++){ pro+=proRef->{i-1}->{$state[$h]}*transitionRef->{state[h]}->[$k]; } proRef−>$i−>$state[$k]=pro*transmitRef−>$state[$k]−>[obsKindNum]; } } foreach mystate(keysproRef->{(scalar @obs)-1}}){ proAfter+=proRef->{(scalar @obs)-1}->{$state}; } proAfter=log(proAfter); my delta=proAfter-$proBefore; proBefore=proAfter; #输出更新后的HMM参数 print OUT time,”t”,delta,”n”; print OUT “initial: “,join(“t”,@initialP),”n”; print OUT “transition matrix: n”; print OUT “t”,join(“t”,@state),”n”; for(my i=0;i<scalar @state;$i++){ print OUT state[i]; for(my j=0;j<scalar @state;$j++){ print OUT “t”,transitionRef−>$state[$i]−>[j]; } print OUT “n”; } print OUT “transmit matrix: n”; print OUT “t”,join(“t”,@obsKind),”n”; for(my i=0;i<scalar @state;$i++){ print OUT state[i]; for(my j=0;j<scalar @obsKind;$j++){ print OUT “t”,transmitRef−>$state[$i]−>[j]; } print OUT “n”; } print OUT “n”; if(delta<threshold){ print OUT time,”t”,delta,”tOvern”; last; } } close OUT or die”$!”; 更多语言版本的实现见网友的总结：http://hi.baidu.com/shinchen2/item/86fdadcd67d63c7189ad9ee3。此外，我在学习的过程中参考了下面这位网友的学习经验(https://www.52nlp.cn/hmm-learn-best-practices-seven-forward-backward-algorithm-5).他写得很通俗易懂，推荐大家看看。 另外，在R语言中专门有一个包HMM用来实现该模型。 […]
博主，你好！我遇到一道题需要利用马尔科夫模型去解，但是因为是管理专业的，第一次接触到这种方法，所以，想请教一下。。。。。
[回复]
看了一上午文中所说的tutorial 看到前向后向时的一头雾水 才发现这里的blog～
[回复]
楼主能不能把这个代码粗略的讲一下，看的很晕啊。不过前面的写的很好，谢谢楼主。
[回复]
博主，你好。我想用隐马尔科夫模型来识别刀具磨损状态，我一直搞不懂观测序列到底是什么，是某一个状态下的观测Ot,用一组特征值表示，还是几个连续状态下的观测O1，O2..OT,如果是几个连续状态下的观测值，那怎么识别啊？
[回复]
想问一下博主，里面BW算法，求前项变量的时候为何要出去scale[t]呢？
[回复]
您好，首先感谢您在HMM的理解上给我的帮助。
有个问题想请教您，我可以用BW算法训练出一个转移矩阵中某些个转移概率为0的HMM么？
就比如说这个umdhmm工具，如果有这种需求的话，怎么修改哪段代码呢？
[回复]