正态分布的前世今生(六)

（六)开疆扩土，正态分布的进一步发展

2.进军近代统计学

花开两朵，各表一枝。上面说了围绕正态分布在概率论中的发展，现在来看看正态分布在数理统计学中发展的故事。 这个故事的领衔主演是 Adolphe Quetelet和高尔顿(Galton)。

由于高斯的工作，正态分布在误差分析迅速确定了自己的定位，有了这么好的工具，我们可能拍脑袋就认为，正态分布很快 就被人们用来分析其它的数据，然而事实却出乎我们的意料，正态分布进入社会领域和自然科学领域，可是经过一番周折的。

首先我要告诉大家一个事实：误差分析和统计学是两个风马牛不相及的两个学科。 当然这个事实存在的时间是19世纪初之前。统计学的产生最初是与“编制国情报告”有关，主要服务于政府部门。 统计学面对的是统计数据，是对多个不同对象的测量；而误差分析研究的是观测数据， 是对同一个对象的多次测量。因此观测数据和 统计数据在当时被认为两种不同行为获取得到的数据，适用于观测数据的规律未必适用于统计数据。 19世纪的统计数据分析处于一个很落后的状态，和概率论没有多少结合。 而概率论的产生主要和赌博相关，发展过程中与误差分析紧密联系， 而与当时的统计学交集非常小。将统计学与概率论真正结合起来推动数理统计学发展的便是我们的统计学巨星Quetelet。

Quetelet这名字或许不如其它数学家那么响亮，估计很多人不熟悉，所以有必要介绍一下。 Quetelet是比利时人，数学博士毕业，年轻的时候曾追谁拉普拉斯学习过概率论。 此人学识渊博，涉猎广泛，脑门上的桂冠包括统计学家、数学家、天文学家、社会学家、 国际统计会议之父、近代统计学之父、数理统计学派创始人。 Quetelet 的最大的贡献就是将法国的古典概率引入统计学，用纯数学的方法对社会现象进行研究。

1831年，Quetelet参与主持新建比利时统计总局的工作。他开始从事有关人口问题的统计学研究。 在这种研究中，Quetelet发现,以往被人们认为杂乱无章的、偶然性占统治地位的社会现象， 如同自然现象一样也具有一定的规律性。 Quetelet 搜集了大量关于人体生理测量的数据，如体重、身高与胸围等，并使用概率统计方法来 对数据进行数据分析。但是当时的统计分析方法遭到了社会学家的质疑， 社会学家们的反对意见主要在于：社会问题 与科学实验不同，其数据一般由观察得到，无法控制且经常不了解其异质因素，这样数据 的同质性连带其分析结果往往就有了问题，于是社会统计工作者就面临一个如何判 断数据同质性的问题。Quetelet大胆地提出：

把一批数据是否能很好地拟合正态分布，作为判断该批数据同质的依据。

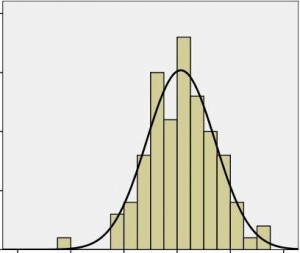
Quetelet提出了一个使用正态曲线拟合数据的方法，并广泛的使用正态分布去拟合各种类型的数据。 由此， Quetelet为正态分布的应用拓展了广阔的舞台。 正态分布如同一把屠龙刀，在Quetelet 的带领下，学者们挥舞着这把宝刀在各个领域披荆斩棘， 攻陷了人口、领土、政治、农业、工业、商业、道德等社会领域， 并进一步攻占天文学、数学、物理学、生物学、社会统计学及气象学等自然科学领域。

正态分布的下一个推动力来自生物学家高尔顿，当正态分布与生物学联姻时，近代统计学迎来了一次大发展。 高尔顿是生物统计学派的奠基人，他的表哥达尔文的巨著《物种起源》问世以后，触动他用统计方法研究遗传进化问题。 受Quetelet的启发，他对正态分布怀有浓厚的兴趣，开始使用正态分布去拟合人的身高、胸围、以至考试成绩等各类数据， 发现正态分布拟合得非常好。他因此相信正态曲线是适用于无数情况的一般法则。

然而，对高尔顿而言，这个无处不在的正态性给他带来一些困惑。他考察了亲子两代的身高数据， 发现遵从同一的正态分布，遗传作为一个显著因素是如何发挥作用的？1877年， 高尔顿设计了一个 叫高尔顿钉板(quincunx, 或者Galton board)的装置，模拟正态分布的性质用于解释遗传现象。

如下图中每一点表示钉在板上的一颗钉子，它们彼此的距离均相等。 当小圆球向下降落过程中，碰到钉子后皆以 $\frac{1}{2}$ 的概率向左或向右滚下。 如果有$n$排钉子，则各槽内最终球的个数服从二项分布 $B(n,1/2)$, 当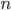 较大的时候，接近正态分布。

高尔顿钉板

设想在此装置的中间某个地方 AB 设一个挡板把小球截住，小球将在AB处聚成正态曲线形状，如果挡板上 有许多阀门，打开一些阀门，则在底部形成多个大小不一的正态分布，而最终的大正态分布正式这些小 正态分布的混合。

高尔顿钉板解释遗传现象

高尔顿利用这个装置创造性的把正态分布的性质用于解释遗传现象。 他解释说身高受到显著因素和其它较小因素的影响，每个因素的影响可以表达为 一个正态分布。遗传作为一个显著因素，类似图中底部大小不一的正态分布中的比较大的正态分布， 而多个大小不一正态分布累加之后其结果任然得到一个正态分布。

高尔顿在研究身高的遗传效应的时候，同时发现一个奇特的现象：高个子父母的子女，其身高有 低于其父母身高的趋势，而矮个子父母的子女，其身高有高于其父母的趋势，即有“回归”到普通人平均身高 去的趋势，这也是“回归”一词最早的含义。高尔顿用二维正态分布去拟合父代和子代身高的数据， 同时引进了回归直线、相关系数的概念，从而开创了回归分析这门技术。

可以说，高尔顿是用统计方法研究生物学的第一人，他用实际行动开拓了Quetelet的思想； 为数理统计学的产生奠定了基础。 无论是 Quetelet 还是高尔顿，他们的统计分析工作都是以正态分布为中心的， 在他们的影响下，正态分布获得了普遍认可和广泛应用，甚至是被滥用， 以至有些学者认为19世纪是正态分布在统计学中占统治地位的时代。

3. 数理统计三剑客

最后，我们来到了20世纪，正态分布的命运如何呢？ 如果说19世纪是正态分布在统计学中独领风骚的话，20世纪则是数理统计学蓬勃发展、百花齐放的时代。 1901年，高尔顿和他的学生卡尔.皮尔逊(Karl Pearson)、韦尔登（W.F.R Weldon) 创办《生物计量(Biometrika)》杂志，成为生物统计学派的一面旗帜，引导了现代数理统计学的大发展。 统计学的重心逐渐由欧洲大陆向英国转移，使英国在以后几十年数理统计学发展的黄金时代充当了领头羊。

在20世纪以前，统计学所处理的数据一般都是大量的、自然采集的，所用的方法以 拉普拉斯中心极限定理为依据，总是归结到正态。到了19世纪末期，数据与正态拟合不好的情况也日渐为人们所注意： 进入20世纪之后，人工试验条件下所得数据的统计分析问题，日渐被人们所重视。 由于试验数据量有限，那种依赖于近似正态分布的传统方法开始招致质疑，这促使人们研 究这种情况下正确的统计方法问题

在这个背景之下，统计学三大分布$\chi^2$分布、$t$分布、$F$分布逐步登上历史舞台。 这三大分布现在的理科本科生都很熟悉。在历史上，这三个分布和来自英国的现代数理 统计学的三大剑客有着密切的关系。

第一位剑客就是卡尔.皮尔逊(Karl Pearson)，手中的宝剑就是$\chi^2$分布。 $\chi^2$分布这把宝剑最早的锻造者其实是物理学家麦克斯韦， 他在推导空气分子的运动速度的分布的时候，发现分子速度在三个坐标轴上的分量是正态分布， 而分子运动速度的平方$v^2$符合自由度为3的$\chi^2$分布。麦克斯韦虽然造出了这把宝剑， 但是真正把它挥舞得得心应手、游刃有余的是皮尔逊。在分布曲线 和数据的拟合优度检验中，$\chi^2$分布可是一个利器，而皮尔逊的这个工作被认为是假设检验的开山之作。 皮尔逊继承了高尔顿的衣钵，统计功力深厚，在19世纪末20世纪初很长的一段时间里，一直被数理统计武林 人士尊为德高望重的第一大剑客。

第二位剑客是戈塞特(Gosset)，笔名是大家都熟悉的学生氏(Student)，而他手中的宝剑是$t$ 分布。戈塞特是化学、数学双学位，依靠自己的化学知识进酿酒厂工作， 工作期间考虑酿酒配方实验中的统计学问题，追谁卡尔.皮尔逊学习了一年的统计学， 最终依靠自己的数学知识打造出了$t$分布这把利剑而青史留名。 1908年，戈塞特提出了正态样本中样本均值和标准差的比值的分布， 并给出了应用上及其重要的第一个分布表。戈塞特在$t$分布的工作是开创了小样本统计学的先河。

第三位剑客是费希尔(R.A.Fisher)，手持$F$分布这把宝剑，在一片荒芜中开拓出方差分析的肥沃土地。 $F$分布就是为了纪念费希尔而用他的名字首字母命名的。 费希尔剑法飘逸，在三位剑客中当属费希尔的天赋最高，各种兵器的使用都得心应手。 费希尔统计造诣极高，受高斯的启发，系统的创立了极大似然估计剑法，这套剑法现在被尊为 统计学参数估计中的第一剑法。

费希尔还未出道，皮尔逊已经是统计学的武林盟主了，两人岁数相差了33岁，而戈塞特介于他们中间。 三人在统计学擂台上难免切磋剑术。费希尔天赋极高，年少气盛；而皮尔逊为人强势， 占着自己武林盟主的地位，难免固执己见，以大欺小；费希尔着实受了皮尔逊不少气。 而戈塞特性格温和，经常在两人之间调和。毕竟是长江后浪推前浪，一代新人换旧人， 在众多擂台比试中，费希尔都技高一筹，而最终取代了皮尔逊成为数理统计学第一大剑客。

由于这三大剑客和统计三大分布的出现，正态分布在数理统计学中不再是一枝独秀， 数理统计的领地基本上是被这三大分布抢走了半壁江山。不过这对正态分布而言并非坏事，我们细看这三大分布的数学细节: 假设独立随机变量 $X_i \sim N(0,1), Y_j \sim N(0,1) (i=1\cdots n, j=1\cdots m)$，则满足 三大分布的随机变量可以如下构造出来

• $\displaystyle \chi_n^2 = X_1^2 + \cdots + X_n^2$
• $\displaystyle t = \frac{Y_1}{\sqrt{\frac{X_1^2 + \cdots + X_n^2}{n}}}$
• $\displaystyle F = \frac{\frac{X_1^2 + \cdots + X_n^2}{n}}{\frac{Y_1^2 + \cdots + Y_m^2}{m}} $

你看这三大分布哪一个不是正态分布的嫡系血脉，没有正态分布就生不出$\chi^2$分布、$t$分布、$F$分布。所以正态 分布在19世纪是武则天，进入二十世纪就学了慈禧太后，垂帘听政了。 或者，换个角度说，一个好汉三个帮，正态分布如果是孤家寡人恐怕也难以雄霸天下， 有了统计学三大分布作为开国先锋为它开疆拓土，正态分布真正成为傲世群雄的君王。

20世纪初，统计学这三大剑客成为了现代数理统计学的奠基人。以哥塞特为先驱，费歇尔为主将， 掀起了小样本理论的革命，事实上提升了正态分布在统计学中的地位。 在数理统计学中，除了以正态分布为基础的小样本理论获得了空前的胜利，其它分布上都没有成功的案例， 这不能不让人对正态分布刮目相看。在随后的发展中，相关回归分析、多元分析、方差分析、因子分析、 布朗运动、高斯过程等等诸多统计分析方法陆续登上了历史舞台， 而这些和正态分布密切相关的方法，成为推动现代统计学飞速发展的一个强大动力。