
3.Quasi-Newton Method
在第2节中我们了解了步长的概念,以及从x_k走到x_k+1点使用line search方法计算步长的方法。不过我们在那里忽略了一个重要的概念,即“方向”。从第2节,我们了解到从每一点x_k走到下一点x_k+1时,需要给出要走的“方向”,只有“方向”确定好之后,才能在此基础上应用line search方法找到对应的“步长”,因此在解决了“步长”计算问题之后,这里我们将和大家一起了解一下每一步的“方向”如何确定。本节分为2大部分,首先我们通过newton method引入方向的概念,在此基础上引入quasi-newton method。然后引入quasi-newton method中的一种重要方法BFGS method,并在BFGS method的基础上介绍用于大规模计算的LBFGS method算法,同时以此结束本节的所有内容。
3.1 Newton Method
我想我们还依稀记得,微积分中用于求一元函数根的Newton法。该方法可用如下所示的图形来描述:
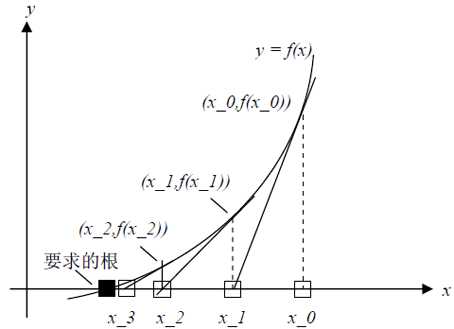
首先我们选择一个初始点x_0并计算获得其对应的f(x_0),然后该方法用曲线y = f(x)在(x_0,f(x_0))的切线近似该曲线,把切线和x轴的交点记作x_1,点x_1通常x_0更接近所要求得根,同样方法用点x_1处的切线近似该曲线,并求取切线和x轴的交点x_2,一直迭代下去,直到找到满足我们所需的充分接近真实跟的解为止。因此Newton法从第k次近似值x_k求得第k+1次近似值x_k+1即为求x_k点处的切线和x轴的交点。
切线方程为:
y – f(x_k) = ▽f (x_k)(x – x_k)
=> 0 – f(x_k) =▽ f(x_k)(x – x_k)
=> ▽f(x_k)*x = ▽f(x_k)*x_k – f(x_k)
=> x = x_k – f(x_k)/▽f (x_k)
因此x_k+1 = x_k – f(x_k)/▽f(x_k) (19)
从上面使用Newton Method求函数根的过程可以发现,首先需要选择一个初始点,并在点处构建一个模型来近似该函数。
切线模型: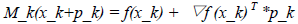
上面使用了相应点处的切线模型来近似函数,然后求取该近似模型的根以便求得更接近函数根的下一个点,该过程一直迭代下去,直到找到根为止。从上面构建每个点处的近似模型可以发现,该模型相对原函数来说简化了很多,因此求解要容易一些。
现在来考虑求取函数的最小值问题,方法类似。首先开始我们选择一个初始点x_0,并构建函数在该点处的一个近似模型,上面求函数根时,我们构建的近似模型为切线模型。这里我们构建一个抛物线模型:
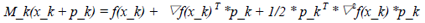
并求解该模型的梯度,同时令其为零,即:▽M_k(x+) = 0,在此基础上求得x+,该值即使得近似模型取得最小值的点。
对抛物线模型M_k求导并令其为零后,可得以下公式:
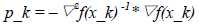 (20)
(20)
因此 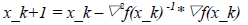 (21)
(21)
从上式可见,使用Newton法时,每一步的方向为p_k,而步长为1。从Newton法方向公式我们不难看出,若使用Newton法,则从每个最小值近似点x_k走到下一个近似点x_k+1的过程中将涉及函数Hessian矩阵▽▽f(x_k) (二阶导)计算,而该Hessian矩阵无法保证在每个点处都是正定的,对正定矩阵来说存在如下不等式:
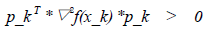 (22)
(22)
由于矩阵无法保证为正定矩阵,因此下式中
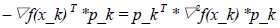 (23)
(23)
p_k无法保证总是为下降方向,即负梯度方向。
从上面的分析可见,Newton Method面临两个问题:
1) Hessian矩阵计算量较大
2) Hessian矩阵无法保证在迭代的过程中始终处于正定状态
为了解决这两个问题,我们引入Quasi-Newton Method。
未完待续:无约束最优化五
注:这个系列的作者是我的师兄jianzhu,他在中文分词、语言模型方面的研究很深入,如果大家对于srilm的源代码感兴趣,可以参考他个人博客上写的“srilm阅读文档系列”,很有帮助。
原创文章,转载请注明出处“我爱自然语言处理”:www.52nlp.cn
本文链接地址:https://www.52nlp.cn/unconstrained-optimization-four
根据文章,我理解这里近似模型如果是“抛物线模型”时,会遇到计算Hessian矩阵的问题,那么,请问为什么是抛物线模型呢?线性模型的话不会遇到这个问题。
[回复]
fandywang 回复:
15 5 月, 2013 at 16:50
这里的Hessian矩阵应该在使用Newton法计算最值过程中(通过导数的导数等于0求解)需要的吧
[回复]
52nlp 回复:
22 5 月, 2013 at 23:01
直接问jianzhu吧
[回复]
zelfendo 回复:
24 4 月, 2014 at 16:55
其实不是构建抛物线方程,是将目标函数展成二阶泰勒展式,拟合原来的曲线
[回复]