无约束最优化三

2.2 a_k步长的选择
　　了解了a_k的合理性之后，就相当于获得了标尺，在此基础上我们可以选择合适的策略来求取a_k。所有的line search过程在计算每一步的a_k时，均需要提供一个初始点a_0，然后再此基础上生成一系列的{a_i}，直到a_i满足2.1节所规定的条件为止，此时该a_k即被确定为a_i，或者未找到一个合适的a_k。这里我们仅介绍目前常用的策略平方插值和立方插值法。因此本节内容分为两部分，2.2.1节介绍选择a_k常用的平方插值和立方插值法，2.2.2节介绍由x_k点到x_k+1点，方向确定为p_k后，步长a_k具体计算过程。

2.2.1 平方立方插值法
　　当给定一个初始步长a_0，若该初始步长满足Wolfe conditions（或strong Wolfe conditions），则a_k被确定为a_0，当前点x_k步长计算过程结束，否则，我们可以在此基础上，利用已知的三个信息Ø(a_0)、Ø(0)、Ø’(0)，构建一个二次（平方）插值多项式来拟合Ø(a_k)。该二次插值多项式如下所示：
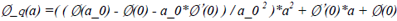(15)
观察上面的二次插值多项式可知，其满足如下插值条件：

Ø_q(0) = Ø(0)　Ø_q’(0) = Ø’(0)　Ø_q(a_0) = Ø(a_0)

对二次插值多项式(15)求导并令其为零，即可获得使得该多项式取得最小值的a值，如下所示：
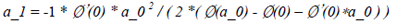(16)
若a_1满足Wolfe conditions（或strong Wolfe conditions），则a_k 被确定为a_1。否则在此基础上构建一个三次（立方）插值多项式，并求得使得该多项式取最小值的a值，该a值的计算公式如下所示：

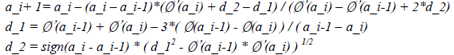
　　　　　　　　　　　　　　　　　　　　　　　　　　　(17)
若a_i+1满足Wolfe conditions（或strong Wolfe conditions），则a_k 被确定为a_i+1，否则一直使用三次插值多项式进行插值拟合。并且选择使用a_i+1对应的Ø (a_i+1)和Ø’(a_i+1)替换a_i-1或a_i相应的值，一旦确定好a_i-1或a_i中的一种后，每次都替换对应的值，如替换a_i-1，则每次都使用新的a_i+1对应的值替换a_i-1，直到找到满足Wolfe conditions（或strong Wolfe conditions）的a_i+1为止，此时a_k被确定为a_i+1，或者没有找到合适的a_i+1。
　　这里有必要简略解释一下为何只使用到三次插值多项式，而没有使用更高阶的插值多项式。原因是三次插值多项式对函数某个点处的具体值有较好的拟合效果，同时又有较好的抗过拟合作用。
　　最后有必要解释一下初始步长a_0的选择，对于Newton或quasi-Newton methods来说，初始步长a_0总是确定为1，该选择确保当满足Wolfe conditions（或strong Wolfe conditions），我们总是选择单位1步长，因为该步长使得Newton或quasi-Newton methods达到较快的收敛速度。计算第零步长时，将初始步长a_0使用如下公式确定：
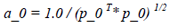　　　　　 (18)
第1步及其以后的初始步长a_0，直接设定为1。

2.2.2 步长a_k计算
　　本节主要做一个总结，即综合前面步长需要满足的条件及步长迭代计算公式给出步长计算的具体过程。下面假设我们处于x_k点，因此要从该点选择一个满足Wolfe (或strong Wolfe) conditions的步长a_k，以便走到下一点x_k+1。因此我们选择初始点a_0 = 1，Newton或quasi-Newton method中初始步长总是选择为1。因此有：

1) 初始化 a_xlefta_yleft0 Ø(a_x) 、 Ø(a_y) 、Ø’(a_x) 、 Ø’(a_y)、a_min、a_max
2) 初始化 a_ilefta_0、Ø’(a_i)、Ø(a_i)
3) 若Ø(a_i) > Ø(a_x)

　说明步长a_i选择的过大，因此使得Ø(a_i)满足Wolfe(或strong Wolfe) conditions的步长a_k应位于a_x和a_i之间，使用平方和立方插值法对a_x和a_i分别进行插值，求取两个新的步长a_quadratic和a_cubic，并取两者之中和a_x较接近的步长，这里假设为a_quadratic，将新的步长设为a_qudratic，同时进行以下操作：

a_y left a_i
Ø(a_y) left Ø(a_i)
Ø’(a_y) left Ø’(a_i)
a_i+1 left a_quadrati

同时在此情况下，说明a_k位于a_x和a_y之间

4) 若Ø’(a_i)* Ø’(a_x) < 0 　　说明步长a_i选择的过大，因此使得Ø(a_i)满足Wolfe(或strong Wolfe) conditions的步长a_k应位于a_x和a_i之间，使用平方和立方插值法对a_x和a_i分别进行插值，求取两个新的步长a_quadratic和a_cubic，并取两者之中和a_i较接近的步长，这里假设为a_quadratic，将新的步长设为a_qudratic，同时进行以下操作：

a_y left a_x
Ø(a_y) left Ø(a_x)
Ø’(a_y) left Ø’(a_x)

a_x left a_i
Ø(a_x) left Ø(a_i)
Ø’(a_x) left Ø’(a_i)

a_i+1 left a_quadrati

同时在此情况下，说明a_k位于a_x和a_y之间

5) 若|Ø’(a_i)| <|Ø’(a_x) | 　　说明步长a_i选择的过小，因此使得Ø(a_i)满足Wolfe(或strong Wolfe) conditions的步长a_k应位于a_i和a_y之间，使用平方和立方插值法对a_x和a_i分别进行插值，求取两个新的步长a_quadratic和a_cubic，并取两者之中和a_i较接近的步长，这里假设为a_quadratic，将新的步长设为a_qudratic，同时进行以下操作：

a_x left a_i
Ø(a_x) left Ø(a_i)
Ø’(a_x) left Ø’(a_i)

a_i+1 left a_quadrati

同时在此情况下，说明a_k位于a_x和a_y之间

6) 若|Ø’(a_i)| ≥|Ø’(a_x) |
　　说明步长a_i选择的过小，若之前已经确定出了a_k所属的范围a_x和a_y，则使得Ø(a_i)满足Wolfe(或strong Wolfe) conditions的步长a_k应位于a_i和a_y之间，使用立方插值法对a_i和a_y进行插值，求取新的步长a_cubic，新的步长设为a_cubic；否则若a_x小于a_i，说明的新的步长不够大，因此将新的步长设置为a_max，若a_x大于等于a_i，则说明新的步长不够小，将其设为a_min，同时进行以下操作：

a_x left a_i
Ø(a_x) left Ø(a_i)
Ø’(a_x) left Ø’(a_i)

if 之前已经确定出了a_k所属的范围a_x和a_y

a_i+1 left a_cubic
else if a_x ＜ a_i
a_i+1 left a_max
else if a_x ≥ a_i
a_i+1 left a_min

7) 计算判断若a_i+1使得以下两式(strong Wolfe condition)均成立：

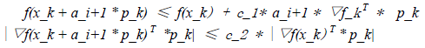
则找到合理的步长a_k，将其设定为a_i+1

a_k left a_i+1

则x_k点步长a_k计算结束。
否则转到2）继续计算合理步长。

未完待续：无约束最优化四

注：这个系列的作者是我的师兄jianzhu，他在中文分词、语言模型方面的研究很深入，如果大家对于srilm的源代码感兴趣，可以参考他个人博客上写的“srilm阅读文档系列”，很有帮助。

原创文章，转载请注明出处“我爱自然语言处理”：www.52nlp.cn

本文链接地址：https://www.52nlp.cn/unconstrained-optimization-three