
2.1 a_k合理性讨论
如下将要讨论关于a_k需要满足的两个条件,当a_k满足这两个条件后,就可以认为从x_k点移动到x_k+1点的步长已经确定下来了。第一个条件为sufficient decrease condition,从直观角度来看,该条件主要要用保证x_k+1点的函数值要小于x_k点的函数值,满足该条件后,才有全局收敛 的可能性。第二个条件为curvature condition,从直观角度来看,该条件主要用于保证x_k点经过步长a_k的移动到达x_k+1后,▽f_k+1小于▽f_k。
2.1.1 sufficient decrease condition
a_k的选择一定要使得函数值满足sufficient decrease condition,该条件可以用如下不等式描述:
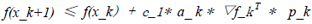 (3)
(3)
将公式(1)代入上式,可得:
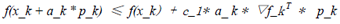 (4)
(4)
这里有必要对上面的不等式做一些解释:
a) f(x_k) 代表函数在第x_k点的值
b) ▽f_k代表函数在第x_k点的梯度
c) p_k代表从第x_k点的走到x_k+1点的方向
d) a_ k代表从第x_k点沿着p_k方向走到x_k+1点步长
e) c_1为常量,需满足 0< c_1 < 1,一般取c_1为1E-4(注:Quasi-Newton Method中要求0< c_1< 0.5)
当p_k为函数下降方向时,有:
▽f_k * p_k < 0 (5)
因此不等式4,即要求:
f(x_k+1) < f(x_k) (6)
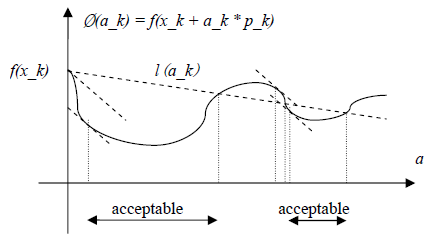
从图形角度看,函数位于第k点时,以上各参数中只有a_k为变量,其他均为常量,因此(4)可以用以下不等式重新描述为:
Ø(a_k) ≤ l(a_k) (7)
其中:
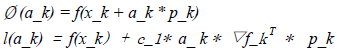
以下为不等式(7)的图形化表示:
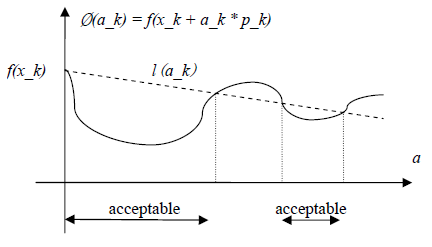
因此只要步长a_k的选择使得函数Ø(a_k)位于acceptable区间,就满足sufficient decrease condition。
2.1.2 curvature condition
a_k的选择一定要使得函数梯度值满足curvature condition,该条件可以用如下不等式描述:
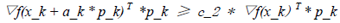 (8)
(8)
即为
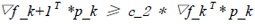 (9)
(9)
这里有必要对上面的不等式做一些解释:
a) ▽f_k+1代表函数在第x_k+1点的梯度
b) ▽f_k代表函数在第x_k点的梯度
c) p_k代表从第k点的走到k+1点的方向
d) c_2为常量,需满足0< c_1 < c_2 < 1,一般取c_2为0.9
当p_k为函数下降方向时,有:
▽f_k * p_k < 0
因此不等式9,即要求:
▽f _k+1 ≥ c_2 * ▽f_k (10)
从图形角度看,不等式10即要求函数在第x_k+1点的变化速度要低于x_k点的变化速度,这一点可以从这两点处的梯度处看出,如下图所示。
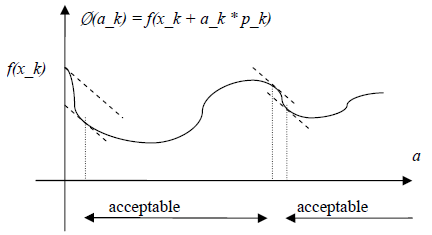
2.1.3 Wolfe conditions
所谓Wolfe conditions即sufficient decrease condition和curvature condition的综合,即a_k需要同时满足如下两个条件:
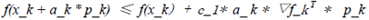 (11)
(11)
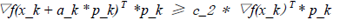 (12)
(12)
图形化表示后,如下图所示:
实际应用中,常常会用到由Wolfe conditions引申出的strong Wolfe conditions,即a_k需要同时满足如下两个条件: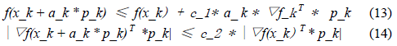
与Wolfe condtions唯一的区别是strong Wolfe condtions避免了▽f(x_k + a_k * p_k)取较大的正值情况。
未完待续:无约束最优化三
注:这个系列的作者是我的师兄jianzhu,他在中文分词、语言模型方面的研究很深入,如果大家对于srilm的源代码感兴趣,可以参考他个人博客上写的“srilm阅读文档系列”,很有帮助。
原创文章,转载请注明出处“我爱自然语言处理”:www.52nlp.cn
本文链接地址:https://www.52nlp.cn/unconstrained-optimization-two
curvature condition 章节的内容,公式8,9,10,12 应该是 小于等于 吧,怎么会是大于等于呢?
[回复]
公式(10)逻辑上就不对,向量不能比较大小。假如改为向量的模,那么如何从公式(8)(9)推导出(10)?回复1楼:(8)(9)的两边都是负数,所以大于号没错。
[回复]
john 回复:
23 2 月, 2014 at 14:20
(10)式大于等于号对?例如2*-1>=3*-1,这个代表式子(9),p_k=-1,这里2<3(式子10)的,所以这个有问题吧。。。
[回复]
8,9是正确的,10除非p_k, 梯度向量都是一个实数时才有这样的结论
[回复]