
六、维特比算法(Viterbi Algorithm)
寻找最可能的隐藏状态序列(Finding most probable sequence of hidden states)
2d.反向指针, 's
's
考虑下面这个网格
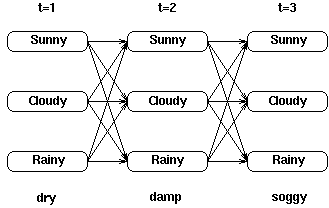
在每一个中间及终止状态我们都知道了局部概率, (i,t)。然而我们的目标是在给定一个观察序列的情况下寻找网格中最可能的隐藏状态序列——因此,我们需要一些方法来记住网格中的局部最佳路径。
(i,t)。然而我们的目标是在给定一个观察序列的情况下寻找网格中最可能的隐藏状态序列——因此,我们需要一些方法来记住网格中的局部最佳路径。
回顾一下我们是如何计算局部概率的,计算t时刻的 's我们仅仅需要知道t-1时刻的
's我们仅仅需要知道t-1时刻的 's。在这个局部概率计算之后,就有可能记录前一时刻哪个状态生成了
's。在这个局部概率计算之后,就有可能记录前一时刻哪个状态生成了 (i,t)——也就是说,在t-1时刻系统必须处于某个状态,该状态导致了系统在t时刻到达状态i是最优的。这种记录(记忆)是通过对每一个状态赋予一个反向指针
(i,t)——也就是说,在t-1时刻系统必须处于某个状态,该状态导致了系统在t时刻到达状态i是最优的。这种记录(记忆)是通过对每一个状态赋予一个反向指针 完成的,这个指针指向最优的引发当前状态的前一时刻的某个状态。
完成的,这个指针指向最优的引发当前状态的前一时刻的某个状态。
形式上,我们可以写成如下的公式
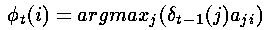
其中argmax运算符是用来计算使括号中表达式的值最大的索引j的。
请注意这个表达式是通过前一个时间步骤的局部概率 's和转移概率计算的,并不包括观察概率(与计算局部概率
's和转移概率计算的,并不包括观察概率(与计算局部概率 's本身不同)。这是因为我们希望这些
's本身不同)。这是因为我们希望这些 's能回答这个问题“如果我在这里,最可能通过哪条路径到达下一个状态?”——这个问题与隐藏状态有关,因此与观察概率有关的混淆(矩阵)因子是可以被忽略的。
's能回答这个问题“如果我在这里,最可能通过哪条路径到达下一个状态?”——这个问题与隐藏状态有关,因此与观察概率有关的混淆(矩阵)因子是可以被忽略的。
2e.维特比算法的优点
使用Viterbi算法对观察序列进行解码有两个重要的优点:
1. 通过使用递归减少计算复杂度——这一点和前向算法使用递归减少计算复杂度是完全类似的。
2.维特比算法有一个非常有用的性质,就是对于观察序列的整个上下文进行了最好的解释(考虑)。事实上,寻找最可能的隐藏状态序列不止这一种方法,其他替代方法也可以,譬如,可以这样确定如下的隐藏状态序列:
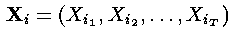
其中
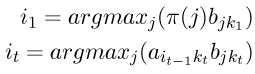
这里,采用了“自左向右”的决策方式进行一种近似的判断,其对于每个隐藏状态的判断是建立在前一个步骤的判断的基础之上(而第一步从隐藏状态的初始向量 开始)。
开始)。
这种做法,如果在整个观察序列的中部发生“噪音干扰”时,其最终的结果将与正确的答案严重偏离。
相反, 维特比算法在确定最可能的终止状态前将考虑整个观察序列,然后通过 指针“回溯”以确定某个隐藏状态是否是最可能的隐藏状态序列中的一员。这是非常有用的,因为这样就可以孤立序列中的“噪音”,而这些“噪音”在实时数据中是很常见的。
指针“回溯”以确定某个隐藏状态是否是最可能的隐藏状态序列中的一员。这是非常有用的,因为这样就可以孤立序列中的“噪音”,而这些“噪音”在实时数据中是很常见的。
3.小结
维特比算法提供了一种有效的计算方法来分析隐马尔科夫模型的观察序列,并捕获最可能的隐藏状态序列。它利用递归减少计算量,并使用整个序列的上下文来做判断,从而对包含“噪音”的序列也能进行良好的分析。
在使用时,维特比算法对于网格中的每一个单元(cell)都计算一个局部概率,同时包括一个反向指针用来指示最可能的到达该单元的路径。当完成整个计算过程后,首先在终止时刻找到最可能的状态,然后通过反向指针回溯到t=1时刻,这样回溯路径上的状态序列就是最可能的隐藏状态序列了。
未完待续:维特比算法4
本文翻译自:http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html
部分翻译参考:隐马尔科夫模型HMM自学
转载请注明出处“我爱自然语言处理”:www.52nlp.cn
本文链接地址:https://www.52nlp.cn/hmm-learn-best-practices-six-viterbi-algorithm-3
请问:该节中2e.-2.那个it的递归表达式里ait-1kt是哪个概率(不好意思,打出公式的格式)?是不是ait-1j
[回复]
52nlp 回复:
7 12 月, 2010 at 21:04
好像ait-1j更合理一些,原文见:
http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/viterbi_algorithm/s1_pg14.html
可能有误,谢谢!
[回复]
2d的最后一段:
请注意这个表达式是通过前一个时间步骤的局部概率delta‘s和转移概率计算的,并不包括观察概率(与计算局部概率delta‘s本身不同)。这是因为我们希望这些phi‘s能回答这个问题“如果我在这里,最可能通过哪条路径到达下一个状态?”
这里翻译是否有误?
我觉得应该翻译成:
“如果我在这里,那我是通过哪条路径到达这个状态的?”
[回复]
切萝卜 回复:
16 5 月, 2011 at 14:59
“如果我在这里,那我最优可能是通过哪条路径到达这个状态的?”
[回复]
简单的想的话, 感觉Viterbi算法和前向算法就是各种条件概率的计算嘛..
[回复]
“自左至右”决策方法中,t时刻索引的计算公式下标是否有误呢?
i(t)=argmaxj(a(i(t-1),j)*b(j,k(t)))
原式中a的下标是i(t-1)和k(t),显然不符合a的定义
[回复]
Conversely, the Viterbi algorithm will look at the whole sequence before deciding on the most likely final state, and then `backtracking' through the f pointers to indicate how it might have arisen. This is very useful in `reading through' isolated noise garbles, which are very common in live data.
相反, 维特比算法在确定最可能的终止状态前将考虑整个观察序列,然后通过phi指针“回溯”以确定某个隐藏状态是否是最可能的隐藏状态序列中的一员。这是非常有用的,因为这样就可以孤立序列中的“噪音”,而这些“噪音”在实时数据中是很常见的。
这段话和博主有点不同,贴一下我自己的理解:
相反, 维特比算法在确定最可能的终止状态前将考虑整个观察序列,然后通过phi指针“回溯”以考察这个隐藏状态序列产生的可能性。这是非常有用的,可以用来辨别实际数据中很常见的孤立的“噪音”片段。
PS:还没有看完全文,可能理解有谬误,暂时在这里存疑
[回复]
有一点不太理解,反向指针那里为什么不需要乘上混淆矩阵的因子。
从编程的角度来讲,在计算局部变量时我已经可以找出取值最大时的j,这个j也就是下一最佳路径的出发点,这时候我是考虑了混淆矩阵的因子的。
[回复]
计算完所有cell的局部概率,相应的最优隐藏状态序列就出来。只需要一个回溯过程将这个序列打印出来就行了。。。为什么还要强行用一个公式表示,,整的我以为这地方又有其他什么相关理论。。。或者我理解错了?
[回复]