五、前向算法（Forward Algorithm）
计算观察序列的概率（Finding the probability of an observed sequence）
2b.计算t=1时的局部概率
's
我们按如下公式计算局部概率：
t ( j )= Pr( 观察状态 | 隐藏状态j ) x Pr(t时刻所有指向j状态的路径）
特别当t=1时，没有任何指向当前状态的路径。故t=1时位于当前状态的概率是初始概率，即Pr(state|t=1)=P(state)，因此，t=1时的局部概率等于当前状态的初始概率乘以相关的观察概率：
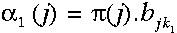
所以初始时刻状态j的局部概率依赖于此状态的初始概率及相应时刻我们所见的观察概率。
2c.计算t>1时的局部概率's
我们再次回顾局部概率的计算公式如下：
t ( j )= Pr( 观察状态 | 隐藏状态j ) x Pr(t时刻所有指向j状态的路径）
我们可以假设（递归地），乘号左边项“Pr( 观察状态 | 隐藏状态j )”已经有了，现在考虑其右边项“Pr(t时刻所有指向j状态的路径）”。
为了计算到达某个状态的所有路径的概率，我们可以计算到达此状态的每条路径的概率并对它们求和，例如：
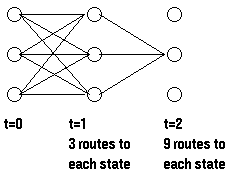
计算所需要的路径数目随着观察序列的增加而指数级递增，但是t-1时刻's给出了所有到达此状态的前一路径概率，因此，我们可以通过t-1时刻的局部概率定义t时刻的's，即：
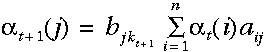
故我们所计算的这个概率等于相应的观察概率（亦即，t+1时在状态j所观察到的符号的概率）与该时刻到达此状态的概率总和——这来自于上一步每一个局部概率的计算结果与相应的状态转移概率乘积后再相加——的乘积。
注意我们已经有了一个仅利用t时刻局部概率计算t+1时刻局部概率的表达式。
现在我们就可以递归地计算给定隐马尔科夫模型(HMM)后一个观察序列的概率了——即通过t=1时刻的局部概率's计算t=2时刻的's，通过t=2时刻的's计算t=3时刻的's等等直到t=T。给定隐马尔科夫模型(HMM)的观察序列的概率就等于t=T时刻的局部概率之和。
2d.降低计算复杂度
我们可以比较通过穷举搜索（评估）和通过递归前向算法计算观察序列概率的时间复杂度。
我们有一个长度为T的观察序列O以及一个含有n个隐藏状态的隐马尔科夫模型l=(
穷举搜索将包括计算所有可能的序列：
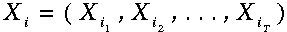
公式
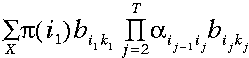
对我们所观察到的概率求和——注意其复杂度与T成指数级关系。相反的，使用前向算法我们可以利用上一步计算的信息，相应地，其时间复杂度与T成线性关系。
注：穷举搜索的时间复杂度是
3.总结
我们的目标是计算给定隐马尔科夫模型HMM下的观察序列的概率——Pr(observations |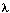
)。
我们首先通过计算局部概率（'s）降低计算整个概率的复杂度，局部概率表示的是t时刻到达某个状态s的概率。
t=1时，可以利用初始概率(来自于P向量）和观察概率Pr(observation|state)（来自于混淆矩阵）计算局部概率；而t>1时的局部概率可以利用t-时的局部概率计算。
因此，这个问题是递归定义的，观察序列的概率就是通过依次计算t=1,2,...,T时的局部概率，并且对于t=T时所有局部概率's相加得到的。
注意，用这种方式计算观察序列概率的时间复杂度远远小于计算所有序列的概率并对其相加（穷举搜索）的时间复杂度。
未完待续：前向算法3
本文翻译自：http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html
部分翻译参考：隐马尔科夫模型HMM自学
转载请注明出处“我爱自然语言处理”：www.52nlp.cn
本文链接地址：https://www.52nlp.cn/hmm-learn-best-practices-five-forward-algorithm-2
个人理解，这里是把需要重复计算的项，存储在了局部概率里，减少了重复计算，是动态规划的思想。
[回复]
admin 回复:
23 8 月, 2009 at 14:11
是这样的，前向算法和维特比算法都利用了动态规划的思想。
[回复]
‘现在我们就可以递归地计算给定隐马尔科夫模型(HMM)后一个观察序列的概率了——即通过t=1时刻的局部概率’s计算t=2时刻的’s，通过t=2时刻的’s计算t=3时刻的’s等等直到t=T。给定隐马尔科夫模型(HMM)的观察序列的概率就等于t=T时刻的局部概率之和。’
你翻译的文章很好，我把原文也看过了。收获很大。
但是有一个问题就是：为什么'给定隐马尔科夫模型(HMM)的观察序列的概率就等于t=T时刻的局部概率之和‘？
我的理解是：整个观察序列的概率等于：每个observation的概率的乘积，也就是：
P(dry)*P(soggy)*P(damp).
但是t=T时刻的局部概率只求出了P(damp)啊，还需要再乘以t=1和t=2时的P(dry)和P(soggy)才是整个观察序列的概率。这里一直比较迷惑，希望得到解答，谢谢！
我对文章的理解是：在求T时刻的局部概率alfa（T）时，已经包含了t=1和t=2时的P(dry)，P(soggy)，所以不用再乘了。但是感觉中间又少了些东西。
[回复]
52nlp 回复:
28 11 月, 2009 at 12:45
首先，你的理解“整个观察序列的概率等于：每个observation的概率的乘积，也就是：
P(dry)*P(soggy)*P(damp)”是有问题的。如果给定了隐藏状态的序列，譬如“sunny,sunny,sunny”，那么观察序列的概率可以等于Pr(dry,damp,soggy | sunny,sunny,sunny),根据独立性假设，可以等价于“B(dry|sunny)*B(damp|sunny)*B(soggy|sunny)”，但是当前的隐藏状态序列是不可知的，所以必须穷举出所有的隐藏状态序列，计算给出的观察序列的概率，并对其求和，也就是：
Pr(dry,damp,soggy | HMM) = Pr(dry,damp,soggy | sunny,sunny,sunny) + Pr(dry,damp,soggy | sunny,sunny ,cloudy) + Pr(dry,damp,soggy | sunny,sunny ,rainy) + . . . . Pr(dry,damp,soggy | rainy,rainy ,rainy)
有27种情况，但是需要注意的是，这个计算过程中除了有上述观察概率的相乘外，还要考虑隐藏状态之间的转移概率，因为隐藏状态之间的转移是不确定的。
还是拿例子说吧，最后一个时刻的局部概率有三个:当隐藏状态为sunny时，局部概率为Pr(dry,damp,soggy|.,.,sunny)；为cloudy时，局部概率为Pr(dry,damp,soggy|.,.,cloudy)；同理，第三个局部概率为(dry,damp,soggy|.,.,rainy)。
其中“.,.”代表的是任意两个隐藏状态之间的组合(3*3)，每个局部概率已经计算好了总的27种情况中的9种情况，所以它们之和就是所有可以穷举的27中情况。
估计你的理解中没有考虑到每种情况计算概率后还有求和，所以觉得其中缺了什么吧！
[回复]
多谢回答！
感觉关键是hidden的state对observation的决定作用没有理解好。这下明白了
[回复]
52nlp 回复:
1 12 月, 2009 at 07:32
不客气，欢迎多来走走！
[回复]
穷举搜索的时间复杂度公式中的2从何何来？
[回复]
52nlp 回复:
29 4 月, 2012 at 09:05
这篇论文中“A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition”有详细的解释，可以看一下。
[回复]
bitwjg 回复:
1 5 月, 2012 at 18:23
好的多谢 🙂
[回复]
博主你好，我有个跟lingandcs 类似的问题。
我刚开始也有跟他一样的想法，即整个观察序列的概率等于：每个observation的概率的乘积，也就是：
P(dry)*P(soggy)*P(damp).
但是后来了解由于dry,soggy,damp有着顺序的前后依赖关系，即状态转移矩阵定义的内容必须考虑在内。
是否可以这样想，完全不考虑隐藏状态的序列，单分析观察序列的状态变化，即类似于
P(dry, soggy)=P(dry)*P(soggy|dry)
P(dry, soggy, cludy) = P(dry ， soggy)* P(cludy | dry, soggy)
？
求指教
[回复]
52nlp 回复:
11 10 月, 2012 at 09:51
P(dry, soggy, cludy)
这个可以按照链式法则展开，但是实际处理的时候需要做一些简化。
[回复]
补充一下，P(soggy|dry)等可由状态转移矩阵求得，
P(soggy|dry)即时间1为soggy,时间2为dry
[回复]
这是动态规划的思想，说是递归不太对吧？如果用递归实现的话，估计就跟穷举法一样慢了
[回复]
52nlp 回复:
22 10 月, 2012 at 18:26
yes，是动态规划。
[回复]
第二个公式，b 的下标是不是 jk_{t+1} ,那个地方图片不清楚，看着像是i+1？但是觉得应该是t+1 才能理解
[回复]
博主你好，看了你的博文，非常有启发，谢谢。有一个关于局部概率的递推的疑问想请教下，望指教。
假设转移矩阵为A，混淆矩阵为B，观察序列为o(1...T)
文中说alpha(t,j) = Pr( o(t) | j ) * Pr(t时刻所有指向j状态的路径），所以
alpha(t,j) = B( j,o(t) ) * Pr(t时刻所有指向j状态的路径）
alpha(t+1,j) = B( j,o(t+1) ) * Pr(t+1时刻所有指向j状态的路径）
= B( j,o(t+1) ) * Sum{Pr(t时刻所有指向i状态的路径)*A(i,j)}
= B( j,o(t+1) ) * Sum{alpha(t,i)/B(i,o(t)) * A(i,j)}
但文中的式子却没有除以B(i,o(t))，所以我觉得
Pr(t时刻所有指向j状态的路径）应该为Pr(t时刻所有指向j状态的路径，且t-1时刻的隐含状态生成观察状态o(t-1)），这样理解的话，后面的Sum{alpha(T,j)}就是观察状态序列的概率就容易理解了，因为每一个时刻都假设了前面的时刻产生了正确的观察状态，所以最后一步产生正确观察状态o(T)的概率即为产生整个序列o(1....T)的概率。
[回复]
请问博主“前向算法2”这篇网页里面的
2d. 降低计算复杂度 块中的穷举搜索，有一个求概率的公式。
这个公式里面的alpha(i(j-1))(i(j))代表了什么意思啊？//括号代表下标。
[回复]
t+1时刻的局部概率公式下标是否有问题呢？
根据https://www.52nlp.cn/hmm-learn-best-practices-four-hidden-markov-models
a(ij)=Pr(x(i,t)|x(j,t-1))
按照以上定义，局部概率是否应该表为：
α(t+1,j)=b(j,t+1,k,t+1)*sum(α(t,i)*a(ji))
[回复]
Eclipse 回复:
22 4 月, 2014 at 15:48
看了后面的内容，下标都是一致的，可能“HMM学习最佳范例四：隐马尔科夫模型”的标注方法仅限于那一节，博主是否标注一下比较好呢~
[回复]
52nlp 回复:
22 4 月, 2014 at 16:04
这个版本已经有很多年了，很多朋友提建议，找个时间我重新做个修订版，谢谢。
[回复]
尊敬的52nlp先生您好，感谢您分享的这么多的文章，对于初学者的我获益匪浅。
简短叙述一下我的学习经历，想请教阁下两个问题：
我在学习完中文分词的基于词典的分词方法之后，也用perl语言很好的实践过了。
因为基于词典的分词方法现已落伍了，于是开始学习基于字标注的中文分词方法。
于是开始看您的一系列《中文分词入门之字标注法》博文。扎进去看了之后觉得一头雾水，于是我觉得应该是基础没有打牢，所以看不懂，于是又转而钻研您的《HMM在自然语言处理中的应用一：词性标注》这一系列的博文，看了之后仍然是一头雾水！于是我继续追根溯源，开始看您这一系列的博文《HMM学习最佳范例》，开始的几篇还浅显易懂，看到这一篇和前一篇，就又感觉非常吃力了！
现在的问题就是：
1、我只是想学习基于字标注的中文分词方法，是否只看《中文分词入门之字标注法》并认真钻研就行了？不应该去追根溯源？
2、如果像这一系列《HMM学习最佳范例》的文章都看不懂，应该怎样进行最初步的学习？或者《HMM学习最佳范例》可以直接当做初学者的入门手册？
还请52nlp先生不吝赐教。
ps: 我是计算机本科毕业，数学功底不是很扎实，有幸跟着导师做课题，想在核心权威刊物上发表一些有关中文分词方面的文章。
[回复]
52nlp 回复:
30 11 月, 2014 at 19:24
不知道你是否在读研？如果读研的话，那就建议你扎扎实实的把基本功打好，包括数学，计算机和英语。即使是发表文章也需要你自己去追踪中文分词领域最新发展的论文等，不是看了这里的几篇博文就可以的。最好从相关的NLP书籍或者课程入手吧：https://www.52nlp.cn/natural-language-processing-primer-books ； http://coursegraph.com/tag/%E8%87%AA%E7%84%B6%E8%AF%AD%E8%A8%80%E5%A4%84%E7%90%86
[回复]
蒙奇奇 回复:
1 12 月, 2014 at 07:23
恩，谢谢了。
读研读的是文科。
现在在高校工作了，因为工作岗位的缘故，又从事这方面的研究。
[回复]
为什么我觉得穷举和前向是一样的复杂度。。。 从初始化开始，到某个T长序列的生成，计算的复杂度是一样的吧？不因为前向存储了结果就简单了啊？
[回复]
请问博主，这一节的算法我能看明白。
就是在计算两个复杂度的公式里，穷举法的那个2，和递归法的那个2分别是怎样计算出的呢？希望能不吝赐教！
[回复]
直接法的计算复杂度为什么是2T*N^T，而不是N^T呢
[回复]
建议复杂度公式记成
N^2 * T
乍看上去像N^(2T)
看了好久，翻了评论，都不知道为什么 ......
[回复]
您好，关于穷举和前向算法的时间复杂度我觉得有点问题
穷举的是2N^T*T
前向算法的是N^2 * T
前向算法比穷举快，只是因为保存了前面的计算结果，那么，如果当T为2的时候，不用保存结果，二者就一样了
如果T为2的时候，那么穷举的时间是 2 * 4 * 2 ， 而前向算法的是 4*2
这样是不是就不一致了
如果在穷举的时候把转移和发射分开来算了，那么前向算法是不是也应该分开，即乘以2？以保证一致呢？
这是我不解的地方，希望指正
然后感谢博主分享的这些知识，对自己很有帮助
[回复]
我按照你给出的原文地址没有找到，显示的是一个大学的主页。
[回复]
52nlp 回复:
5 7 月, 2018 at 23:06
9年前翻译的文章，看起来原文已经有变化了
[回复]
存在几个问题：
（1）前向算法1中，关于穷举算法的计算公式写错了。应该是所有可能的隐藏状态序列与观察状态序列的联合概率的和，也即是网友“jiaqi”评论的那样。同时，联合概率P(AB)如果按照乘法概率展开成P(A|B)P(B)，那么会更加直观，即通过计算每个可能的隐藏序列条件下观察状态出现的概率，并与这个隐藏状态序列出现的概率相乘，然后再求所有情况（穷举）的和。
（2）其实问题（1）的错误是致命性的错误，因为后面提出的递归降低复杂度的算法，实际上与穷举算法要解决的是同一个问题，要计算的概率也是同一个概率。递归降低复杂度的方法，无非将穷举算法的计算公式做了拆解和复用，它最终计算的也是所有可能情况下的概率之和。但原作者和翻译都没有发现这个问题，以至于后面的算法不好理解。
（3）要理解递归降低复杂度的方法，需要知道文中定义的“局部概率”是为了递归计算的需要，人为构造的一个概率，它的实际意义并不是像作者解释的那样，表示t时刻到达某个状态s的概率。而它实际上是概率计算过程中的一个中间“计算状态”，或者更像是考虑了状态序列发生关系之后的隐藏状态序列与观察状态序列的联合概率，只不过作者用αt(j)来表示这个概率，但它一定不能理解为到达某个状态s的概率。
[回复]