
斯坦福大学在三月份开设了一门“深度学习与自然语言处理”的课程:CS224d: Deep Learning for Natural Language Processing,授课老师是青年才俊 Richard Socher,以下为相关的课程笔记。
第四讲:词窗口分类和神经网络(Word Window Classification and Neural Networks)
推荐阅读材料:
- [UFLDL tutorial]
- [Learning Representations by Backpropogating Errors]
- 第四讲Slides [slides]
- 第四讲视频 [video]
以下是第四讲的相关笔记,主要参考自课程的slides,视频和其他相关资料。
本讲概览
- 分类问题背景
- 在分类任务中融入词向量
- 窗口分类和交叉熵误差推导技巧
- 一个单层的神经网络
- 最大间隔损失和反向传播
分类问题定义
- 一般情况下我们会有一个训练模型用的样本数据集
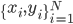
- 其中$x_i$是输入,例如单词(标识或者向量),窗口内容,句子,文档等
- $y_i$是我们希望预测的分类标签,例如情绪指标,命名实体,买卖决定等
分类问题直窥
- 训练集:${\{x_i, y_i\}}^N_{i=1}$
- 一个简单的例子
- 一个固定的2维词向量分类
- 使用逻辑回归
- ->线性决策边界->
- 从机器学习的角度来看:假设x是固定的,仅仅更新的是逻辑回归的权重W意味着仅仅修改的是决策边界
分类问题符号定义
- 一般的机器学习问题: 仅仅更新逻辑回归的权重意味着仅仅更新的是决策边界
- 数据集${\{x_i, y_i\}}^N_{i=1}$的损失函数
- 其中对于每一个数据对$(x_i, y_i)$:
- 我们可以将f写成矩阵符号形式: $f = Wx$
分类问题:正则化
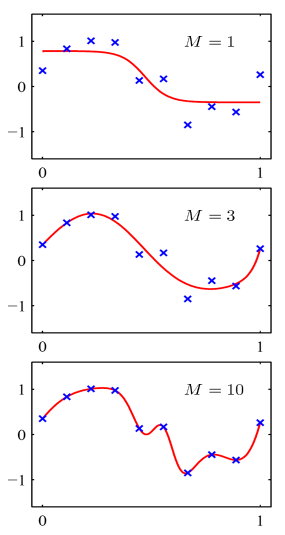
- 通常情况下任何一个数据集上完整的损失函数都会包含一个针对所有参数的正则化因子
- 正则化可以防止过多的特征导致的过拟合问题(另一种解决方案是一个强有力/深度模型)
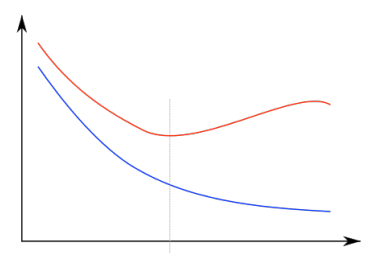
- 上图中x轴代表了更强有力的模型后者更多的模型迭代次数
- 蓝色代表训练集误差,红色代表测试集误差
机器学习优化问题
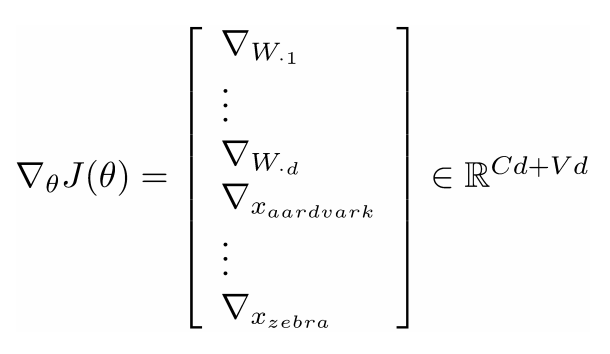
- 对于一般的机器学习问题$\theta$常常只包含了W的列数:
- 所以我们仅仅更新决策边界
引入词向量
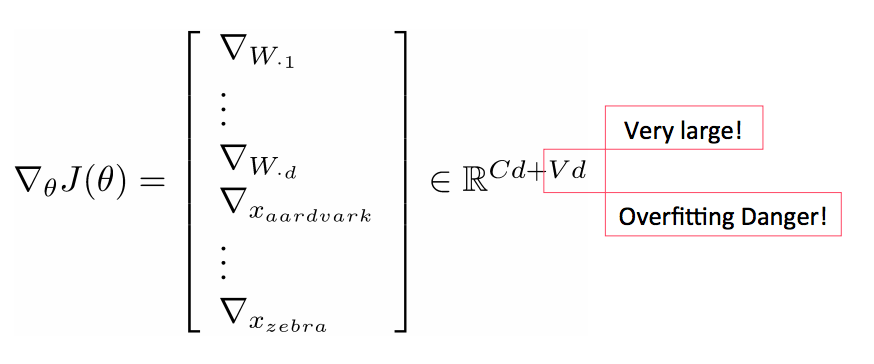
- 在深度学习中既要学习W也要学习词向量x:
重新训练词向量会丧失泛化能力
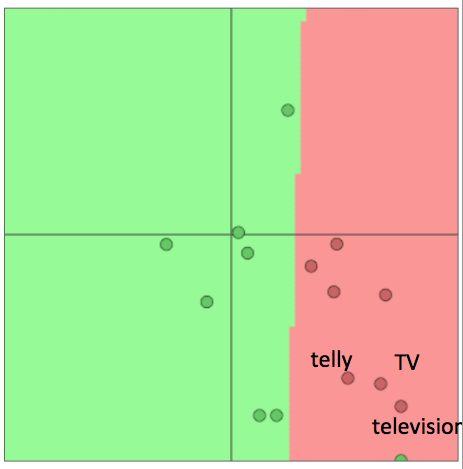
- 例子:针对电影评价情感数据(movie review sentiment)训练逻辑回归模型,在训练集里我们有单词"TV"和"telly"
- 在测试集里我们有单词“television”
- 原本它们是相似的单词(来自于已经训练的词向量模型)
- 当我们重新训练的时候会发生什么?
重新训练词向量会丧失泛化能力续
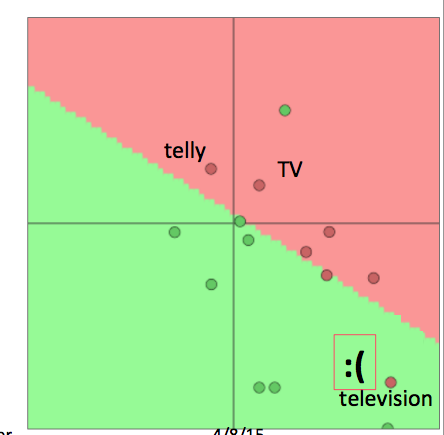
- 当我们重新训练词向量模型的时候会发生什么?
- 在训练集中的单词会被重新安排到合适的位置
- 在已经训练的词向量模型中但是不在训练集中的单词将保留在原来的位置
- 对于上例, "TV"和"telly"会被重新安排,而"television"则保留在原位,尴尬的事情就发生了:
- 总之:
- 如果你只有一个很小的训练集,不要训练词向量模型
- 如果你有一个足够大的训练集,那么对于相应的任务来说训练词向量模型是有益的
词向量概念回顾
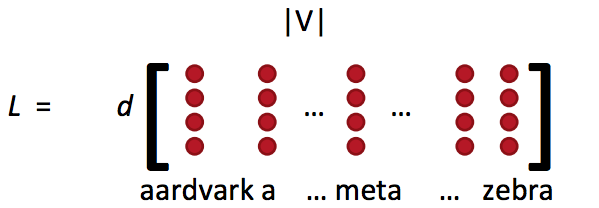
- 词向量矩阵L也被称为查询表
- Word vectors(词向量)= word embeddings(词嵌入) = word representations(mostly)
- 类似于word2vec或者GloVe的方法得到:
- 这就是词特征$x_{word}$
- 通常通过词向量矩阵L和one-hot向量e相乘得到单个的词向量:
窗口分类
- 单个单词的分类任务很少
- 在上下文中解决歧义问题
- 例子1:
- 例子2:
- 思路:将对一个单词进行分类的问题扩展到对其临近词和上下文窗口进行分类
- 例如命名实体问题有4个类别:人名,地名,机构名和其他
- 已经有很多方法在尝试对一个上下文中的单词进行分类,例如将窗口内的单词(向量)进行平均化处理,但是这样会失去位置信息
- 以下介绍一种常用的对窗口(上下文)中单词进行分类的方法
- 对于窗口中的单词打上标签同时把它前后的单词向量进行拼接然后训练一个分类器
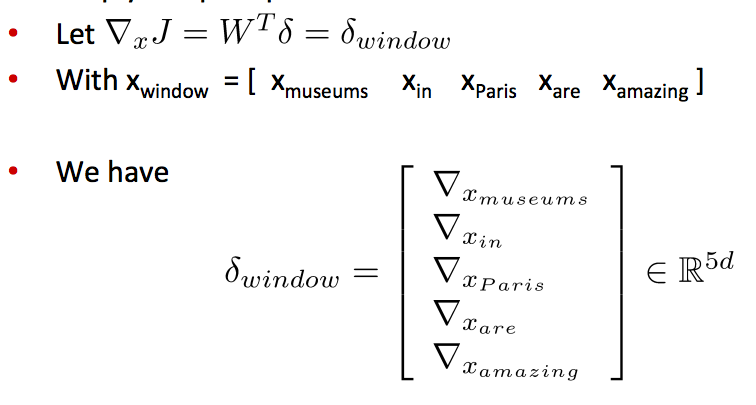
- 例子:对于一个句子上下文中的"Paris"进行分类,窗口长度为2
- 结果得到的窗口向量 $x_{window}=x \in R^{5d}$ , 是一个列向量
简单的窗口分类器: Softmax
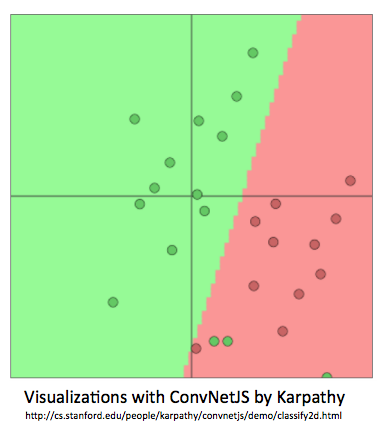
- 在得到窗口向量$x=x_{window}$的情况下,我们可以和之前一样使用softmax分类器
- 但是如何更新词向量?
- 简单的回答:和之前一样进行求导
- 更长的回答:让我们一起来一步一步进行推导
- 定义:
- $\widehat{y}$: softmax 概率输出向量
- t: 目标概率分布
- $f=Wx \in R^c $, 其中$f_c$是f向量的第c个因子
- 第一次看到是不是觉得很难,下面给出一下提示(tips)
更新拼接的词向量:Tips
更新拼接的词向量
- 窗口向量梯度的维度是多少?
- X是整个拼接的词向量窗口,5倍的d维度向量,所以对于x的求导后依然有相同的向量维度(5d)
- 对整个窗口向量的更新和梯度推导可以简单的分解到对每一个词向量的推导:
- 这将保留词向量的原始位置信息有助于一些NLP任务,例如命名实体识别
- 例如,模型将会学习到出现在中心词前面的$x_{in}$常常表示中心词是一个地名(location)
在训练窗口向量时丢失了什么信息?
矩阵实现的一些注解
- 在softmax中有两个代价昂贵的运算: 矩阵运算 f = Wx 和 exp指数运算
- 在做同样的数学运算时for循环永远没有矩阵运算有效
- 样例代码 -->
- 遍历词向量 VS 将它们拼接为一个大的矩阵 然后分别和softmax的权重矩阵相乘
- 运行结果:
- 结果证明矩阵相乘$C \times X$更有效
- 矩阵运算更优雅更棒
- 应该更多的去测试你的代码速度
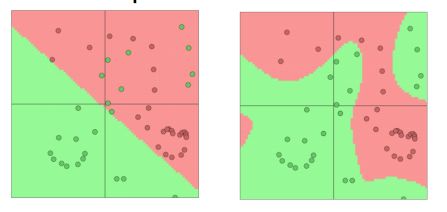
softmax(=逻辑回归)并不是强有力的
神经网络更胜一筹
从逻辑回归到神经网络--神经网络解密
- 神经网络有自己的术语定义集,就像SVM一样
- 但是如果你了解softmax的运行机制,那你就已经了解了一个基本的神经元的运行机制
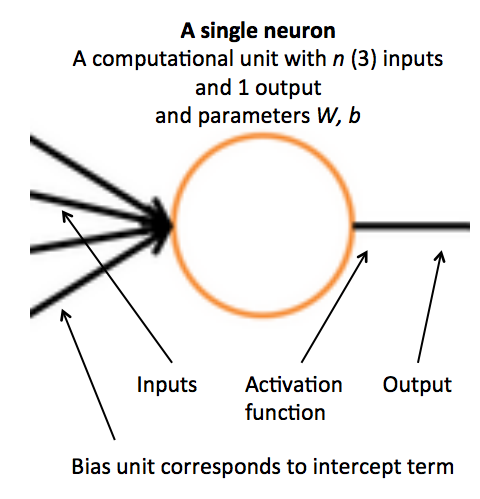
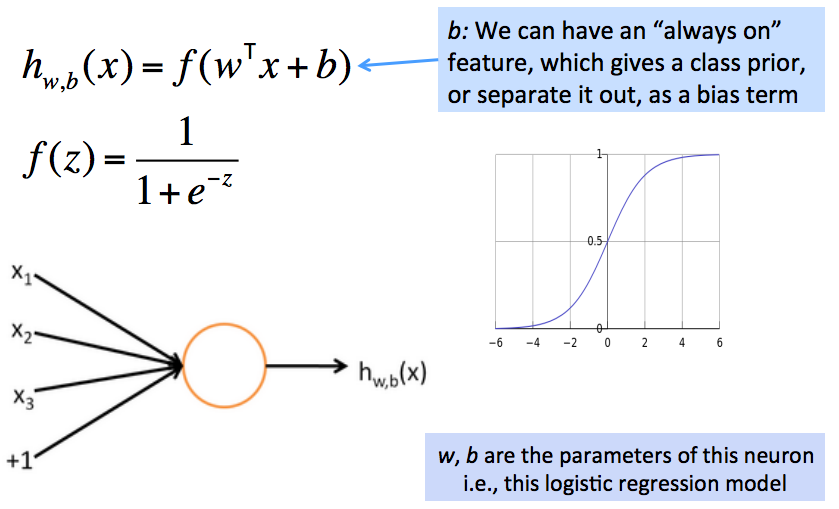
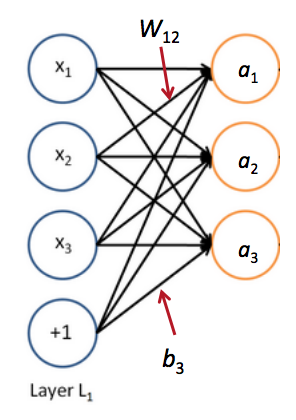
- 例子:一个神经元就是一个基础的运算单位,拥有n(3)个输入和一个输出,参数是W, b
一个神经元本质上是一个二元逻辑回归单元
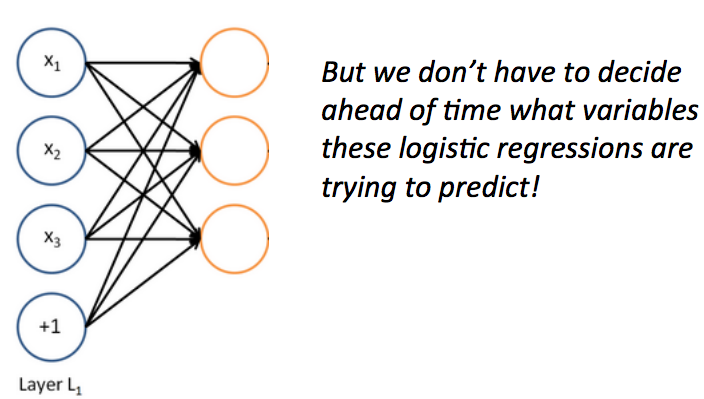
一个神经网络等价于同时运行了很多逻辑回归单元
神经网络中单层的矩阵符号表示
为什么需要非线性的f
一个更牛的窗口分类器
- 基于神经网络进行修正
- 单个(神经网络)层是一个线性层(函数)和非线性函数的组合
- 神经网络激活函数$\alpha$可以用来计算一些函数
- 例如,一个softmax概率分布或者一个没有归一化的打分函数可以是这样的:
总结:前馈网络计算
下一讲
- 训练一个基于窗口(向量)的神经网络模型
- 进行更复杂的深度推导-->反向传播算法
- 这样我们就有了所有的基础工具去学习一个更复杂的深度模型:)
注:原创文章,转载请注明出处及保留链接“我爱自然语言处理”:https://www.52nlp.cn
本文链接地址:斯坦福大学深度学习与自然语言处理第四讲:词窗口分类和神经网络:https://www.52nlp.cn/?p=8694
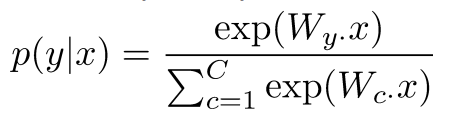
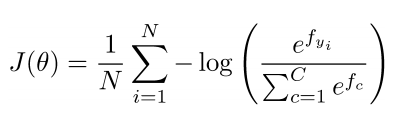
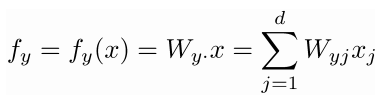

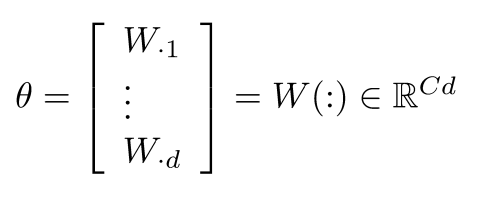
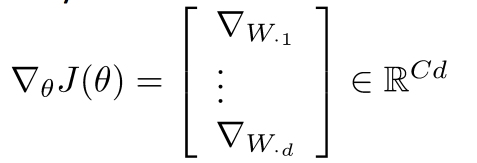




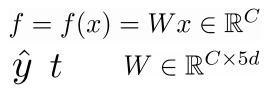
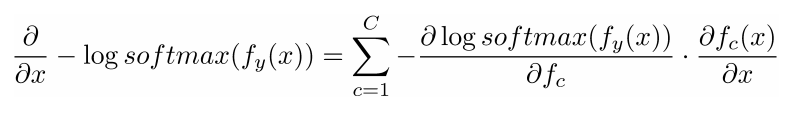
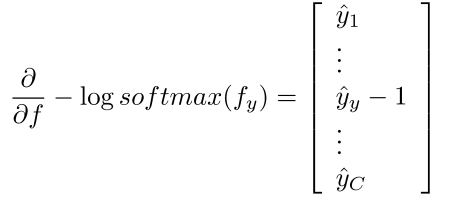
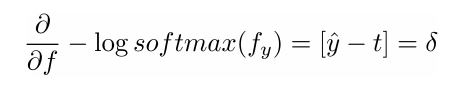
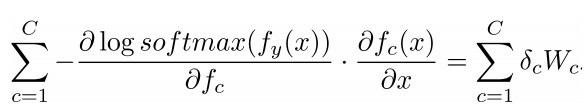
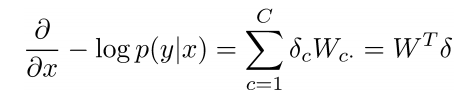
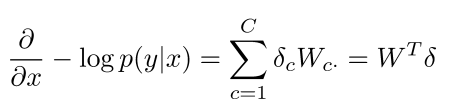
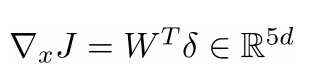

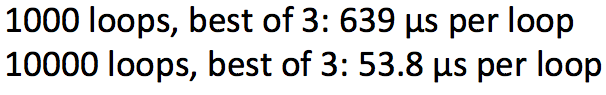




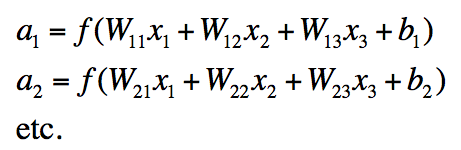
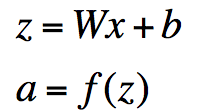
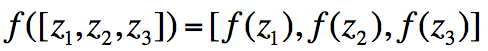
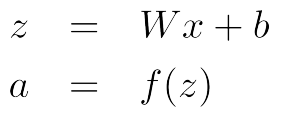
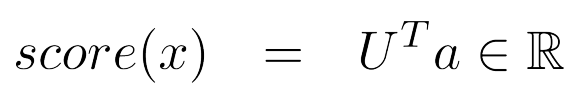
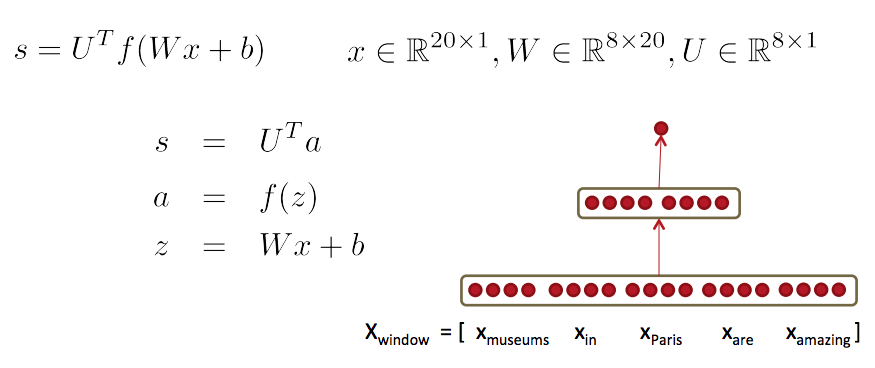
请问Socher在讲这个project的时候是要对X,W都要优化的,那么具体实现的时候,是对X,W同时做优化,还是有其他处理?
[回复]
好棒,不过为什么后面的都没有更新了??
[回复]
52nlp 回复:
23 3 月, 2016 at 11:00
太忙了
[回复]
希望楼主早日更新
[回复]
你好, 我刚刚看完你的斯坦福大学深度学习与自然语言处理第四讲:词窗口分类和神经网络,请问之后的更新有吗?谢谢!!!
[回复]
52nlp 回复:
20 2 月, 2018 at 08:46
没了,建议你直接看最新的课件和课程,更新比较快
[回复]