
蒙特·卡罗方法(Monte Carlo method)也称统计模拟方法,通过重复随机采样模拟对象的概率与统计的问题,在物理、化学、经济学和信息技术领域均具有广泛应用。拒绝采样(reject sampling)就是针对复杂问题的一种随机采样方法。
首先举一个简单的例子介绍Monte Carlo方法的思想。
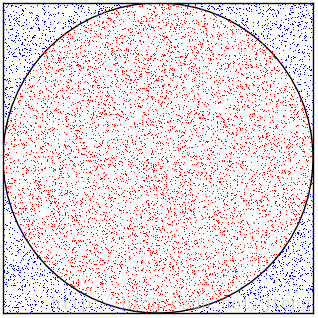
假设要估计圆周率 $\pi$ 的值,选取一个边长为1的正方形,在正方形内作一个内切圆,那么我们可以计算得出,圆的面积与正方形面积之比为 $\pi/4$ 。现在在正方形内随机生成大量的点,如图1所示,落在圆形区域内的点标记为红色,在圆形区域之外的点标记为蓝色,那么圆形区域内的点的个数与所有点的个数之比,可以认为近似等于 $\pi/4$ 。因此,Monte Carlo方法是通过随机采样的方式,以频率估计概率。
简单分布的采样,如均匀分布、高斯分布、Gamma分布等,在计算机中都已经实现,但是对于复杂问题的采样,就需要采取一些策略, 拒绝采样就是一种基本的采样策略,其采样过程如下:
给定一个概率分布 $p(z)=\dfrac{1}{Z_p}\tilde{p}(z)$ 其中 $\tilde{p}(z)$ 已知 $Z_p$ 为归一化常数,是未知的。要对该分布进行拒绝采样。首先定义一个参考分布 $G$ ,概率密度函数 $g(x)$ ,该分布可选均匀分布或高斯分布等。另外再定义一个辅助分布 $U(0,1)$ ,为均匀分布。然后引入常数 $k$ 使得对所有的 $z$ 满足 $kg(z)\le\tilde{p}(z)$ ,然后开始进行采样,在每次采样中先从 $g(z)$ 中采样一个 $z_0$ ,然后在区间 $[0, kg(z_0)]$ 里进行均匀采样,得到 $u_0$ 。如果 $u_0<\tilde{p}(z_0)$ ,则接受,保留该采样值,否则拒绝,舍弃该采样值。最后得到的数据就是对该分布的一个近似采样。
所以使用接受-拒绝采样可以得到采样的概率分布。拒绝采样的目的就是在每个采样点用一个拒绝分布来包含接受分布,通过计算接受概率来表示采样的分布。从而在随机游走的过程中用接受-拒绝采样得到复杂分布,python代码参考如下:
def node2vec_walk2(self, walk_length, start_node):
"""
Reference:
KnightKing: A Fast Distributed Graph Random Walk Engine
http://madsys.cs.tsinghua.edu.cn/publications/SOSP19-yang.pdf
"""
def rejection_sample(inv_p, inv_q, nbrs_num):
upper_bound = max(1.0, max(inv_p, inv_q))
lower_bound = min(1.0, min(inv_p, inv_q))
shatter = 0
second_upper_bound = max(1.0, inv_q)
if (inv_p > second_upper_bound):
shatter = second_upper_bound / nbrs_num
upper_bound = second_upper_bound + shatter
return upper_bound, lower_bound, shatter
G = self.G
alias_nodes = self.alias_nodes
inv_p = 1.0 / self.p
inv_q = 1.0 / self.q
walk = [start_node]
while len(walk) < walk_length:
cur = walk[-1]
cur_nbrs = list(G.neighbors(cur))
if len(cur_nbrs) > 0:
if len(walk) == 1:
walk.append(
cur_nbrs[alias_sample(alias_nodes[cur][0], alias_nodes[cur][1])])
else:
upper_bound, lower_bound, shatter = rejection_sample(
inv_p, inv_q, len(cur_nbrs))
prev = walk[-2]
prev_nbrs = set(G.neighbors(prev))
while True:
prob = random.random() * upper_bound
if (prob + shatter >= upper_bound):
next_node = prev
break
next_node = cur_nbrs[alias_sample(
alias_nodes[cur][0], alias_nodes[cur][1])]
if (prob < lower_bound):
break
if (prob < inv_p and next_node == prev):
break
_prob = 1.0 if next_node in prev_nbrs else inv_q
if (prob < _prob):
break
walk.append(next_node)
else:
break
return walk
